Difference between revisions of "Trigonometric equations involving a single trig function"
Rylee.taylor (talk | contribs) m (adding word) |
|||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| + | '''Trigonometric equations''' are equations including trigonometric functions. If they have only such functions and constants, then the solution involves finding an unknown which is an argument to a trigonometric function. | ||
| + | |||
| + | ==Basic trigonometric equations== | ||
| + | ===sin(''x'') = n=== | ||
| + | <div style="padding-left: 1em; float: right"> | ||
| + | {| border="1" cellspacing="0" cellpadding="5" style="text-align: center" | ||
| + | |colspan="2"| [[Image:Sin unit circle.svg|300px]] | ||
| + | |- | ||
| + | ! <math>n</math> !! <math>\sin(x)=n</math> | ||
| + | |- | ||
| + | | <math>|n|<1</math> | ||
| + | | <math>\begin{matrix}x=\alpha+2k\pi \\ | ||
| + | x=\pi-\alpha+2k\pi \\ | ||
| + | \alpha\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\end{matrix}</math> | ||
| + | |- | ||
| + | | <math>n=-1</math> | ||
| + | | <math>x=-\begin{matrix}\frac{\pi}{2}\end{matrix}+2k\pi</math> | ||
| + | |- | ||
| + | | <math>n=0</math> | ||
| + | | <math>x=k\pi</math> | ||
| + | |- | ||
| + | | <math>n=1</math> | ||
| + | | <math>x=\begin{matrix}\frac{\pi}{2}\end{matrix}+2k\pi</math> | ||
| + | |- | ||
| + | | <math>|n|>1</math> | ||
| + | | <math>x\in\varnothing</math> | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | The equation <math>\sin(x)=n</math> has solutions only when <math>n</math> is within the interval <math>[-1,1]</math> . If <math>n</math> is within this interval, then we first find an <math>\alpha</math> such that: | ||
| + | :<math>\alpha=\arcsin(n)</math> | ||
| + | The solutions are then: | ||
| + | :<math>x=\alpha+2k\pi</math> | ||
| + | :<math>x=\pi-\alpha+2k\pi</math> | ||
| + | Where <math>k</math> is an integer. | ||
| + | |||
| + | In the cases when <math>n</math> equals 1, 0 or -1 these solutions have simpler forms which are summarized in the table on the right. | ||
| + | |||
| + | For example, to solve: | ||
| + | :<math>\sin\bigl(\tfrac{x}{2}\bigr)=\frac{\sqrt3}{2}</math> | ||
| + | First find <math>\alpha</math> : | ||
| + | :<math>\alpha=\arcsin\bigl(\tfrac{\sqrt3}{2}\bigr)=\frac{\pi}{3}</math> | ||
| + | Then substitute in the formulae above: | ||
| + | :<math>\frac{x}{2}=\frac{\pi}{3}+2k\pi</math> | ||
| + | |||
| + | :<math>\frac{x}{2}=\pi-\frac{\pi}{3}+2k\pi</math> | ||
| + | Solving these linear equations for <math>x</math> gives the final answer: | ||
| + | :<math>x=\frac{2\pi}{3}(1+6k)</math> | ||
| + | |||
| + | :<math>x=\frac{4\pi}{3}(1+3k)</math> | ||
| + | Where <math>k</math> is an integer. | ||
| + | |||
| + | <div style="clear: both"></div> | ||
| + | |||
| + | ===cos(''x'') = n=== | ||
| + | <div style="padding-left: 1em; float: right"> | ||
| + | {| border="1" cellspacing="0" cellpadding="5" style="text-align: center" | ||
| + | |colspan="2"| [[Image:Cos unit circle.svg]] | ||
| + | |- | ||
| + | ! <math>n</math> !! <math>\cos(x)=n</math> | ||
| + | |- | ||
| + | | <math>|n|<1</math> | ||
| + | | <math>\begin{matrix}x=\pm\alpha+2k\pi \\ | ||
| + | \alpha\in[0,\pi]\end{matrix}</math> | ||
| + | |- | ||
| + | | <math>n=-1</math> | ||
| + | | <math>x=\pi+2k\pi</math> | ||
| + | |- | ||
| + | | <math>n=0</math> | ||
| + | | <math>x=\begin{matrix}\frac{\pi}{2}\end{matrix}+k\pi</math> | ||
| + | |- | ||
| + | | <math>n=1</math> | ||
| + | | <math>x=2k\pi</math> | ||
| + | |- | ||
| + | | <math>|n|>1</math> | ||
| + | | <math>x\in\varnothing</math> | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | Like the sine equation, an equation of the form <math>\cos(x)=n</math> only has solutions when n is in the interval <math>[-1,1]</math> . To solve such an equation we first find one angle <math>\alpha</math> such that: | ||
| + | :<math>\alpha=\arccos(n)</math> | ||
| + | Then the solutions for <math>x</math> are: | ||
| + | :<math>x=\pm\alpha+ 2k\pi</math> | ||
| + | Where <math>k</math> is an integer. | ||
| + | |||
| + | Simpler cases with <math>n</math> equal to 1, 0 or -1 are summarized in the table on the right. | ||
| + | <div style="clear: both"></div> | ||
| + | |||
| + | ===tan(''x'') = n=== | ||
| + | <div style="padding-left: 1em; float: right"> | ||
| + | {| border="1" cellspacing="0" cellpadding="5" style="text-align: center" | ||
| + | |colspan="2"| [[Image:Tan unit circle.svg]] | ||
| + | |- | ||
| + | ! <math>n!</math> !! <math>\tan(x)=n</math> | ||
| + | |- | ||
| + | | General<br/>case | ||
| + | | <math>\begin{matrix}x=\alpha+k\pi \\ | ||
| + | \alpha\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\end{matrix}</math> | ||
| + | |- | ||
| + | | <math>n=-1</math> | ||
| + | | <math>x=-\begin{matrix}\frac{\pi}{4}\end{matrix}+k\pi</math> | ||
| + | |- | ||
| + | | <math>n=0</math> | ||
| + | | <math>x=k\pi</math> | ||
| + | |- | ||
| + | | <math>n=1</math> | ||
| + | | <math>x=\begin{matrix}\frac{\pi}{4}\end{matrix}+k\pi</math> | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | An equation of the form <math>\tan(x)=n</math> has solutions for any real <math>n</math> . To find them we must first find an angle <math>\alpha</math> such that: | ||
| + | :<math>\alpha=\arctan(n)</math> | ||
| + | After finding <math>\alpha</math> , the solutions for <math>x</math> are: | ||
| + | :<math>x=\alpha+k\pi</math> | ||
| + | When <math>n</math> equals 1, 0 or -1 the solutions have simpler forms which are shown in the table on the right. | ||
| + | <div style="clear: both"></div> | ||
| + | |||
| + | ===cot(''x'') = n=== | ||
| + | <div style="padding-left: 1em; float: right"> | ||
| + | {| border="1" cellspacing="0" cellpadding="5" style="text-align: center" | ||
| + | |colspan="2"| [[Image:Cot unit circle.svg]] | ||
| + | |- | ||
| + | ! <math>n</math> !! <math>\cot(x)=n</math> | ||
| + | |- | ||
| + | | General<br/>case | ||
| + | | <math>\begin{matrix}x=\alpha+k\pi \\ | ||
| + | \alpha\in\left[0;\pi\right]\end{matrix}</math> | ||
| + | |- | ||
| + | | <math>n=-1</math> | ||
| + | | <math>x=-\begin{matrix}\frac{3\pi}{4}\end{matrix}+k\pi</math> | ||
| + | |- | ||
| + | | <math>n=0</math> | ||
| + | | <math>x=\begin{matrix}\frac{\pi}{2}\end{matrix}+k\pi</math> | ||
| + | |- | ||
| + | | <math>n=1</math> | ||
| + | | <math>x=\begin{matrix}\frac{\pi}{4}\end{matrix}+k\pi</math> | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | The equation <math>\cot(x)=n</math> has solutions for any real <math>n</math> . To find them we must first find an angle <math>\alpha</math> such that: | ||
| + | :<math>\alpha=\arccot(n)</math> | ||
| + | After finding <math>\alpha</math> , the solutions for <math>x</math> are: | ||
| + | :<math>x=\alpha+k\pi</math> | ||
| + | When <math>n</math> equals 1, 0 or -1 the solutions have simpler forms which are shown in the table on the right. | ||
| + | <div style="clear: both"></div> | ||
| + | |||
| + | ===csc(''x'') = n and sec(''x'') = n=== | ||
| + | The trigonometric equations <math>\csc(x)=n</math> and <math>\sec(x)=n</math> can be solved by transforming them to other basic equations: | ||
| + | :<math>\csc(x)=n\ \Leftrightarrow\ \frac{1}{\sin(x)}=n\ \Leftrightarrow\ \sin(x)=\frac{1}{n}</math> | ||
| + | :<math>\sec(x)=n\ \Leftrightarrow\ \frac{1}{\cos(x)}=n\ \Leftrightarrow\ \cos(x)=\frac{1}{n}</math> | ||
| + | |||
| + | ==Further examples== | ||
| + | Generally, to solve trigonometric equations we must first transform them to a basic trigonometric equation using the [[../Trigonometric_Identities_Reference|trigonometric identities]]. This sections lists some common examples. | ||
| + | |||
| + | ===''a'' sin(''x'')+''b'' cos(''x'') = ''c''=== | ||
| + | To solve this equation we will use the identity: | ||
| + | :<math>a\sin(x)+b\cos(x)=\sqrt{a^2+b^2}\sin(x+\alpha)</math> | ||
| + | |||
| + | :<math>\alpha=\begin{cases}\arctan\bigl(\frac{b}{a}\bigr), & \mbox{if } a>0 \\ \pi+\arctan\bigl(\frac{b}{a}\bigr), & \mbox{if } a<0 \end{cases}</math> | ||
| + | The equation becomes: | ||
| + | :<math>\sqrt{a^2+b^2}\sin(x+\alpha)=c</math> | ||
| + | |||
| + | :<math>\sin(x+\alpha)=\frac{c}{\sqrt{a^2+b^2}}</math> | ||
| + | |||
| + | This equation is of the form <math>\sin(x)=n</math> and can be solved with the formulae given above. | ||
| + | |||
| + | For example we will solve: | ||
| + | :<math>\sin(3x)-\sqrt3\cos(3x)=-\sqrt3</math> | ||
| + | In this case we have: | ||
| + | :<math>a=1,b=-\sqrt3</math> | ||
| + | :<math>\sqrt{a^2+b^2}=\sqrt{1^2+\Big(-\sqrt3\Big)^2}=2</math> | ||
| + | :<math>\alpha=\arctan\Big(-\sqrt3\Big)=-\frac{\pi}{3}</math> | ||
| + | Apply the identity: | ||
| + | :<math>2\sin\left(3x-\frac{\pi}{3}\right)=-\sqrt3</math> | ||
| + | :<math>\sin\left(3x-\frac{\pi}{3}\right)=-\frac{\sqrt3}{2}</math> | ||
| + | So using the formulae for <math>\sin(x)=n</math> the solutions to the equation are: | ||
| + | :<math>3x-\frac{\pi}{3}=-\frac{\pi}{3}+2k\pi\ \Leftrightarrow\ x=\frac{2k\pi}{3}</math> | ||
| + | |||
| + | :<math>3x-\frac{\pi}{3}=\pi+\frac{\pi}{3}+2k\pi\ \Leftrightarrow\ x=\frac{\pi}{9}(6k+5)</math> | ||
| + | Where <math>k</math> is an integer. | ||
| + | |||
| + | ==Resources== | ||
* [https://mathresearch.utsa.edu/wikiFiles/MAT1093/Trigonometric%20equations%20involving%20a%20single%20trig%20function/Esparza%201093%20Notes%203.3A.pdf Trigonometric equations involving a single trig function]. Written notes created by Professor Esparza, UTSA. | * [https://mathresearch.utsa.edu/wikiFiles/MAT1093/Trigonometric%20equations%20involving%20a%20single%20trig%20function/Esparza%201093%20Notes%203.3A.pdf Trigonometric equations involving a single trig function]. Written notes created by Professor Esparza, UTSA. | ||
* [https://mathresearch.utsa.edu/wikiFiles/MAT1093/Trigonometric%20equations%20involving%20a%20single%20trig%20function/Esparza%201093%20Notes%203.3ACont.pdf Trigonometric equations involving a single trig function continued]. Written notes created by Professor Esparza, UTSA. | * [https://mathresearch.utsa.edu/wikiFiles/MAT1093/Trigonometric%20equations%20involving%20a%20single%20trig%20function/Esparza%201093%20Notes%203.3ACont.pdf Trigonometric equations involving a single trig function continued]. Written notes created by Professor Esparza, UTSA. | ||
| + | |||
| + | == Licensing == | ||
| + | Content obtained and/or adapted from: | ||
| + | * [https://en.wikibooks.org/wiki/Trigonometry/Solving_Trigonometric_Equations Solving Trigonometric Equations, Wikibooks: Trigonometry] under a CC BY-SA license | ||
Latest revision as of 16:48, 28 October 2021
Trigonometric equations are equations including trigonometric functions. If they have only such functions and constants, then the solution involves finding an unknown which is an argument to a trigonometric function.
Contents
Basic trigonometric equations
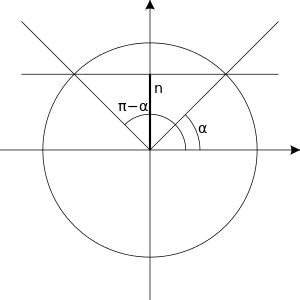
sin(x) = n
The equation has solutions only when is within the interval . If is within this interval, then we first find an such that:
The solutions are then:
Where is an integer.
In the cases when equals 1, 0 or -1 these solutions have simpler forms which are summarized in the table on the right.
For example, to solve:
First find :
Then substitute in the formulae above:
Solving these linear equations for gives the final answer:
Where is an integer.
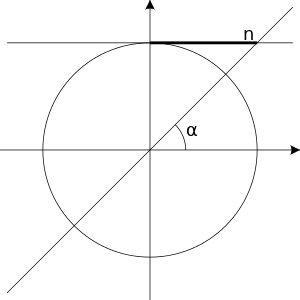
cos(x) = n
Like the sine equation, an equation of the form only has solutions when n is in the interval . To solve such an equation we first find one angle such that:
Then the solutions for are:
Where is an integer.
Simpler cases with equal to 1, 0 or -1 are summarized in the table on the right.
tan(x) = n
An equation of the form has solutions for any real . To find them we must first find an angle such that:
After finding , the solutions for are:
When equals 1, 0 or -1 the solutions have simpler forms which are shown in the table on the right.
cot(x) = n
The equation has solutions for any real . To find them we must first find an angle such that:
After finding , the solutions for are:
When equals 1, 0 or -1 the solutions have simpler forms which are shown in the table on the right.
csc(x) = n and sec(x) = n
The trigonometric equations and can be solved by transforming them to other basic equations:
Further examples
Generally, to solve trigonometric equations we must first transform them to a basic trigonometric equation using the [[../Trigonometric_Identities_Reference|trigonometric identities]]. This sections lists some common examples.
a sin(x)+b cos(x) = c
To solve this equation we will use the identity:
The equation becomes:
This equation is of the form and can be solved with the formulae given above.
For example we will solve:
In this case we have:
Apply the identity:
So using the formulae for the solutions to the equation are:
Where is an integer.
Resources
- Trigonometric equations involving a single trig function. Written notes created by Professor Esparza, UTSA.
- Trigonometric equations involving a single trig function continued. Written notes created by Professor Esparza, UTSA.
Licensing
Content obtained and/or adapted from:
- Solving Trigonometric Equations, Wikibooks: Trigonometry under a CC BY-SA license



![{\displaystyle {\begin{matrix}x=\alpha +2k\pi \\x=\pi -\alpha +2k\pi \\\alpha \in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1a3e9f50511c58a1b5da92a54ebaa528586f4b0)








![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)














![{\displaystyle {\begin{matrix}x=\pm \alpha +2k\pi \\\alpha \in [0,\pi ]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb327bcece984447ffb90d738e9f5c2246d7375d)








![{\displaystyle {\begin{matrix}x=\alpha +k\pi \\\alpha \in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/091023c5ebe89e390dc7b3c08dc2aafd52f739cb)





![{\displaystyle {\begin{matrix}x=\alpha +k\pi \\\alpha \in \left[0;\pi \right]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a09654bc73208cf0114b0bbebf26b68271c20ad0)

















