Uniform Continuity

The graph of $f(x)={\tfrac {1}{x}}$ escapes the top and/or bottom of the ${\text{height}}\times {\text{width}}=2\varepsilon \times 2\delta$ window, however small the $\delta$, so $f(x)$ is not uniformly continuous. The function $g(x)={\sqrt {x}}$, on the other hand, is uniformly continuous.

In mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f(x) and f(y) be as close to each other as we please by requiring only that x and y be sufficiently close to each other; unlike ordinary continuity, where the maximum distance between f(x) and f(y) may depend on x and y themselves.

Continuous functions can fail to be uniformly continuous if they are unbounded on a finite domain, such as $f(x)={\tfrac {1}{x}}$ on (0,1), or if their slopes become unbounded on an infinite domain, such as $f(x)=x^{2}$ on the real line. However, any Lipschitz map between metric spaces is uniformly continuous, in particular any isometry (distance-preserving map).

Although ordinary continuity can be defined for functions between general topological spaces, defining uniform continuity requires more structure. The concept relies on comparing the sizes of neighbourhoods of distinct points, so it requires a metric space, or more generally a uniform space.

Definition for functions on metric spaces

Given metric spaces $(X,d_{1})$ and $(Y,d_{2})$, a function $f:X\to Y$ is called uniformly continuous if for every real number $\varepsilon >0$ there exists real $\delta >0$ such that for every $x,y\in X$ with $d_{1}(x,y)<\delta$, we have that $d_{2}(f(x),f(y))<\varepsilon$.

If X and Y are subsets of the real line, d₁ and d₂ can be the standard one-dimensional Euclidean distance, yielding the definition: for all $\varepsilon >0$ there exists a $\delta >0$ such that for all $x,y\in X,|x-y|<\delta \implies |f(x)-f(y)|<\varepsilon$.

The difference between uniform continuity, versus ordinary continuity at every point, is that in uniform continuity the value of $\delta$ depends only on $\varepsilon$ and not on the point in the domain.

Local continuity versus global uniform continuity

Continuity itself is a local property of a function—that is, a function f is continuous, or not, at a particular point, and this can be determined by looking only at the values of the function in an (arbitrarily small) neighbourhood of that point. When we speak of a function being continuous on an interval, we mean only that it is continuous at each point of the interval. In contrast, uniform continuity is a global property of f, in the sense that the standard definition refers to pairs of points rather than individual points. On the other hand, it is possible to give a definition that is local in terms of the natural extension f* (the characteristics of which at nonstandard points are determined by the global properties of f), although it is not possible to give a local definition of uniform continuity for an arbitrary hyperreal-valued function, see below.

The mathematical statements that a function is continuous on an interval I and the definition that a function is uniformly continuous on the same interval are structurally very similar. Continuity of a function for every point x of an interval can thus be expressed by a formula starting with the quantification

$\forall x\in I\;\forall \varepsilon >0\;\exists \delta >0\;\forall y\in I:\,|x-y|<\delta \,\Rightarrow \,|f(x)-f(y)|<\varepsilon \,,$

whereas for uniform continuity, the order of the first, second, and third quantifiers are rotated:

$\forall \varepsilon >0\;\exists \delta >0\;\forall x,y\in I:\,|x-y|<\delta \,\Rightarrow \,|f(x)-f(y)|<\varepsilon$

Thus for continuity at each point, one takes an arbitrary point x, and then there must exist a distance δ,

$\cdots \forall x\,\exists \delta \cdots ,$

while for uniform continuity a single δ must work uniformly for all points x (and y):

$\cdots \exists \delta \,\forall x\,\forall y\cdots .$

Examples and counterexamples

• Every Lipschitz continuous map between two metric spaces is uniformly continuous. In particular, every function which is differentiable and has bounded derivative is uniformly continuous. More generally, every Hölder continuous function is uniformly continuous.
• Despite being nowhere differentiable, the Weierstrass function is uniformly continuous
• Every member of a uniformly equicontinuous set of functions is uniformly continuous.
• The tangent function is continuous on the interval (−π/2, π/2) but is not uniformly continuous on that interval.
• The exponential function x $\scriptstyle \mapsto$ e^x is continuous everywhere on the real line but is not uniformly continuous on the line.

Properties

Every uniformly continuous function is continuous, but the converse does not hold. Consider for instance the function $f\colon \mathbb {R} \rightarrow \mathbb {R} ,x\mapsto x^{2}$. Given an arbitrarily small positive real number $\varepsilon$, uniform continuity requires the existence of a positive number $\delta$ such that for all $x_{1},x_{2}$ with $|x_{1}-x_{2}|<\delta$, we have $|f(x_{1})-f(x_{2})|<\varepsilon$. But

$f\left(x+{\frac {\delta }{2}}\right)-f(x)=2x\cdot {\frac {\delta }{2}}+{\frac {\delta ^{2}}{4}},$

and for all sufficiently large x this quantity is greater than $\varepsilon$.

Any absolutely continuous function is uniformly continuous. On the other hand, the Cantor function is uniformly continuous but not absolutely continuous.

The image of a totally bounded subset under a uniformly continuous function is totally bounded. However, the image of a bounded subset of an arbitrary metric space under a uniformly continuous function need not be bounded: as a counterexample, consider the identity function from the integers endowed with the discrete metric to the integers endowed with the usual Euclidean metric.

The Heine–Cantor theorem asserts that every continuous function on a compact set is uniformly continuous. In particular, if a function is continuous on a closed bounded interval of the real line, it is uniformly continuous on that interval. The Darboux integrability of continuous functions follows almost immediately from this theorem.

If a real-valued function $f$ is continuous on $[0,\infty )$ and $\lim _{x\to \infty }f(x)$ exists (and is finite), then $f$ is uniformly continuous. In particular, every element of $C_{0}(\mathbb {R} )$, the space of continuous functions on $\mathbb {R}$ that vanish at infinity, is uniformly continuous. This is a generalization of the Heine-Cantor theorem mentioned above, since $C_{c}(\mathbb {R} )\subset C_{0}(\mathbb {R} )$.

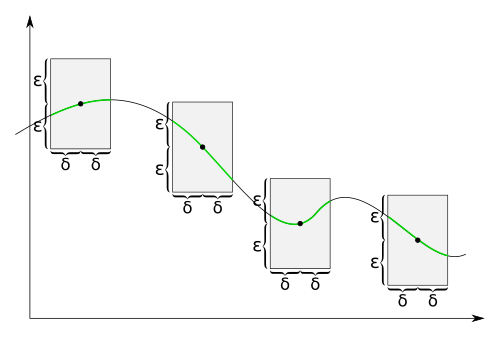
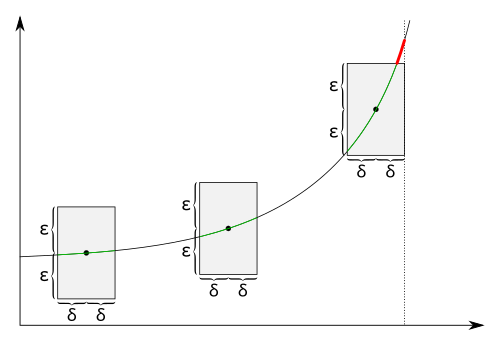
Visualization

For a uniformly continuous function, there is for every given $\varepsilon >0$ a $\delta >0$ such that two values $f(x)$ and $f(y)$ have a maximal distance $\varepsilon$ whenever $x$ and $y$ do not differ for more than $\delta$. Thus we can draw around each point $(x,f(x))$ of the graph a rectangle with height $2\varepsilon$ and width $2\delta$ so that the graph lies completely inside the rectangle and not directly above or below. For functions that are not uniformly continuous, this isn't possible. The graph might lie inside the rectangle for certain midpoints on the graph but there are always midpoints of the rectangle on the graph where the function lies above or below the rectangle.

• 

  For uniformly continuous functions, there is for each $\varepsilon >0$ a $\delta >0$ such that when we draw a rectangle around each point of the graph with width $2\delta$ and height $2\varepsilon$, the graph lies completely inside the rectangle.

• 

  For functions that are not uniformly continuous, there is an $\varepsilon >0$ such that regardless of the $\delta >0$ there are always points on the graph, when we draw a $2\varepsilon \times 2\delta$ rectangle around it, there are values directly above or below the rectangle. There might be midpoints where the graph is completely inside the rectangle but this is not true for every midpoint.

Licensing

Content obtained and/or adapted from:

• Uniform continuity, Wikipedia under a CC BY-SA license