Vectors, Matrices, and Gauss-Jordan Elimination
Contents
- 1 Vectors
- 1.1 Representations
- 1.2 Basic properties
- 2 Dot Product
- 3 Matrices
- 4 Gauss-Jordan Elimination
- 5 Licensing
Vectors
In mathematics, physics and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector or spatial vector) is a geometric object that has magnitude (or length) and direction. Vectors can be added to other vectors according to vector algebra. A Euclidean vector is frequently represented by a ray (a directed line segment), or graphically as an arrow connecting an initial point A with a terminal point B, and denoted by .
A vector is what is needed to "carry" the point A to the point B; the Latin word vector means "carrier". It was first used by 18th century astronomers investigating planetary revolution around the Sun. The magnitude of the vector is the distance between the two points, and the direction refers to the direction of displacement from A to B. Many algebraic operations on real numbers such as addition, subtraction, multiplication, and negation have close analogues for vectors, operations which obey the familiar algebraic laws of commutativity, associativity, and distributivity. These operations and associated laws qualify Euclidean vectors as an example of the more generalized concept of vectors defined simply as elements of a vector space.
Vectors play an important role in physics: the velocity and acceleration of a moving object and the forces acting on it can all be described with vectors. Many other physical quantities can be usefully thought of as vectors. Although most of them do not represent distances (except, for example, position or displacement), their magnitude and direction can still be represented by the length and direction of an arrow. The mathematical representation of a physical vector depends on the coordinate system used to describe it. Other vector-like objects that describe physical quantities and transform in a similar way under changes of the coordinate system include pseudovectors and tensors.
Representations
Vectors are usually denoted in lowercase boldface, as in , and , or in lowercase italic boldface, as in a. (Uppercase letters are typically used to represent matrices.) Other conventions include or a, especially in handwriting. Alternatively, some use a tilde (~) or a wavy underline drawn beneath the symbol, e.g. , which is a convention for indicating boldface type. If the vector represents a directed distance or displacement from a point A to a point B (see figure), it can also be denoted as or AB. In German literature, it was especially common to represent vectors with small fraktur letters such as .
Vectors are usually shown in graphs or other diagrams as arrows (directed line segments), as illustrated in the figure. Here, the point A is called the origin, tail, base, or initial point, and the point B is called the head, tip, endpoint, terminal point or final point. The length of the arrow is proportional to the vector's magnitude, while the direction in which the arrow points indicates the vector's direction.
On a two-dimensional diagram, a vector perpendicular to the plane of the diagram is sometimes desired. These vectors are commonly shown as small circles. A circle with a dot at its centre (Unicode U+2299 ⊙) indicates a vector pointing out of the front of the diagram, toward the viewer. A circle with a cross inscribed in it (Unicode U+2297 ⊗) indicates a vector pointing into and behind the diagram. These can be thought of as viewing the tip of an arrow head on and viewing the flights of an arrow from the back.
In order to calculate with vectors, the graphical representation may be too cumbersome. Vectors in an n-dimensional Euclidean space can be represented as coordinate vectors in a Cartesian coordinate system. The endpoint of a vector can be identified with an ordered list of n real numbers (n-tuple). These numbers are the coordinates of the endpoint of the vector, with respect to a given Cartesian coordinate system, and are typically called the scalar components (or scalar projections) of the vector on the axes of the coordinate system.
As an example in two dimensions (see figure), the vector from the origin O = (0, 0) to the point A = (2, 3) is simply written as
The notion that the tail of the vector coincides with the origin is implicit and easily understood. Thus, the more explicit notation is usually deemed not necessary (and is indeed rarely used).
In three dimensional Euclidean space (or R3), vectors are identified with triples of scalar components:
This can be generalised to n-dimensional Euclidean space (or Rn).
These numbers are often arranged into a column vector or row vector, particularly when dealing with matrices, as follows:
Another way to represent a vector in n-dimensions is to introduce the standard basis vectors. For instance, in three dimensions, there are three of them:
or
where a1, a2, a3 are called the vector components (or vector projections) of a on the basis vectors or, equivalently, on the corresponding Cartesian axes x, y, and z (see figure), while a1, a2, a3 are the respective scalar components (or scalar projections).
In introductory physics textbooks, the standard basis vectors are often denoted instead (or , in which the hat symbol ^ typically denotes unit vectors). In this case, the scalar and vector components are denoted respectively ax, ay, az, and ax, ay, az (note the difference in boldface). Thus,
The notation ei is compatible with the index notation and the summation convention commonly used in higher level mathematics, physics, and engineering.
Decomposition or resolution
As explained above, a vector is often described by a set of vector components that add up to form the given vector. Typically, these components are the projections of the vector on a set of mutually perpendicular reference axes (basis vectors). The vector is said to be decomposed or resolved with respect to that set.
The decomposition or resolution of a vector into components is not unique, because it depends on the choice of the axes on which the vector is projected.
Moreover, the use of Cartesian unit vectors such as as a basis in which to represent a vector is not mandated. Vectors can also be expressed in terms of an arbitrary basis, including the unit vectors of a cylindrical coordinate system () or spherical coordinate system (). The latter two choices are more convenient for solving problems which possess cylindrical or spherical symmetry, respectively.
The choice of a basis does not affect the properties of a vector or its behaviour under transformations.
A vector can also be broken up with respect to "non-fixed" basis vectors that change their orientation as a function of time or space. For example, a vector in three-dimensional space can be decomposed with respect to two axes, respectively normal, and tangent to a surface (see figure). Moreover, the radial and tangential components of a vector relate to the radius of rotation of an object. The former is parallel to the radius and the latter is orthogonal to it.
In these cases, each of the components may be in turn decomposed with respect to a fixed coordinate system or basis set (e.g., a global coordinate system, or inertial reference frame).
Basic properties
The following section uses the Cartesian coordinate system with basis vectors
Equality
Two vectors are said to be equal if they have the same magnitude and direction. Equivalently they will be equal if their coordinates are equal. So two vectors
Opposite, parallel, and antiparallel vectors
Two vectors are opposite if they have the same magnitude but opposite direction. So two vectors
Addition and subtraction
Assume now that a and b are not necessarily equal vectors, but that they may have different magnitudes and directions. The sum of a and b is
The addition may be represented graphically by placing the tail of the arrow b at the head of the arrow a, and then drawing an arrow from the tail of a to the head of b. The new arrow drawn represents the vector a + b, as illustrated below:
This addition method is sometimes called the parallelogram rule because a and b form the sides of a parallelogram and a + b is one of the diagonals. If a and b are bound vectors that have the same base point, this point will also be the base point of a + b. One can check geometrically that a + b = b + a and (a + b) + c = a + (b + c).
The difference of a and b is
Subtraction of two vectors can be geometrically illustrated as follows: to subtract b from a, place the tails of a and b at the same point, and then draw an arrow from the head of b to the head of a. This new arrow represents the vector (-b) + a, with (-b) being the opposite of b, see drawing. And (-b) + a = a − b.
Scalar multiplication
A vector may also be multiplied, or re-scaled, by a real number r. In the context of conventional vector algebra, these real numbers are often called scalars (from scale) to distinguish them from vectors. The operation of multiplying a vector by a scalar is called scalar multiplication. The resulting vector is
Intuitively, multiplying by a scalar r stretches a vector out by a factor of r. Geometrically, this can be visualized (at least in the case when r is an integer) as placing r copies of the vector in a line where the endpoint of one vector is the initial point of the next vector.
If r is negative, then the vector changes direction: it flips around by an angle of 180°. Two examples (r = −1 and r = 2) are given below:
Scalar multiplication is distributive over vector addition in the following sense: r(a + b) = ra + rb for all vectors a and b and all scalars r. One can also show that a − b = a + (−1)b.
Length
The length or magnitude or norm of the vector a is denoted by ‖a‖ or, less commonly, |a|, which is not to be confused with the absolute value (a scalar "norm").
The length of the vector a can be computed with the Euclidean norm,
which is a consequence of the Pythagorean theorem since the basis vectors e1, e2, e3 are orthogonal unit vectors.
This happens to be equal to the square root of the dot product, discussed below, of the vector with itself:
Unit vector
A unit vector is any vector with a length of one; normally unit vectors are used simply to indicate direction. A vector of arbitrary length can be divided by its length to create a unit vector. This is known as normalizing a vector. A unit vector is often indicated with a hat as in â.
To normalize a vector a = (a1, a2, a3), scale the vector by the reciprocal of its length ‖a‖. That is:
Zero vector
The zero vector is the vector with length zero. Written out in coordinates, the vector is (0, 0, 0), and it is commonly denoted , 0, or simply 0. Unlike any other vector, it has an arbitrary or indeterminate direction, and cannot be normalized (that is, there is no unit vector that is a multiple of the zero vector). The sum of the zero vector with any vector a is a (that is, 0 + a = a).
Dot product
The dot product of two vectors a and b (sometimes called the inner product, or, since its result is a scalar, the scalar product) is denoted by a ∙ b, and is defined as:
where θ is the measure of the angle between a and b (see trigonometric function for an explanation of cosine). Geometrically, this means that a and b are drawn with a common start point, and then the length of a is multiplied with the length of the component of b that points in the same direction as a.
The dot product can also be defined as the sum of the products of the components of each vector as
Cross product
The cross product (also called the vector product or outer product) is only meaningful in three or seven dimensions. The cross product differs from the dot product primarily in that the result of the cross product of two vectors is a vector. The cross product, denoted a × b, is a vector perpendicular to both a and b and is defined as
where θ is the measure of the angle between a and b, and n is a unit vector perpendicular to both a and b which completes a right-handed system. The right-handedness constraint is necessary because there exist two unit vectors that are perpendicular to both a and b, namely, n and (−n).
The cross product a × b is defined so that a, b, and a × b also becomes a right-handed system (although a and b are not necessarily orthogonal). This is the right-hand rule.
The length of a × b can be interpreted as the area of the parallelogram having a and b as sides.
The cross product can be written as
For arbitrary choices of spatial orientation (that is, allowing for left-handed as well as right-handed coordinate systems) the cross product of two vectors is a pseudovector instead of a vector (see below).
Scalar triple product
The scalar triple product (also called the box product or mixed triple product) is not really a new operator, but a way of applying the other two multiplication operators to three vectors. The scalar triple product is sometimes denoted by (a b c) and defined as:
It has three primary uses. First, the absolute value of the box product is the volume of the parallelepiped which has edges that are defined by the three vectors. Second, the scalar triple product is zero if and only if the three vectors are linearly dependent, which can be easily proved by considering that in order for the three vectors to not make a volume, they must all lie in the same plane. Third, the box product is positive if and only if the three vectors a, b and c are right-handed.
In components (with respect to a right-handed orthonormal basis), if the three vectors are thought of as rows (or columns, but in the same order), the scalar triple product is simply the determinant of the 3-by-3 matrix having the three vectors as rows
The scalar triple product is linear in all three entries and anti-symmetric in the following sense:
Conversion between multiple Cartesian bases
All examples thus far have dealt with vectors expressed in terms of the same basis, namely, the e basis {e1, e2, e3}. However, a vector can be expressed in terms of any number of different bases that are not necessarily aligned with each other, and still remain the same vector. In the e basis, a vector a is expressed, by definition, as
The scalar components in the e basis are, by definition,
In another orthonormal basis n = {n1, n2, n3} that is not necessarily aligned with e, the vector a is expressed as
and the scalar components in the n basis are, by definition,
The values of p, q, r, and u, v, w relate to the unit vectors in such a way that the resulting vector sum is exactly the same physical vector a in both cases. It is common to encounter vectors known in terms of different bases (for example, one basis fixed to the Earth and a second basis fixed to a moving vehicle). In such a case it is necessary to develop a method to convert between bases so the basic vector operations such as addition and subtraction can be performed. One way to express u, v, w in terms of p, q, r is to use column matrices along with a direction cosine matrix containing the information that relates the two bases. Such an expression can be formed by substitution of the above equations to form
Distributing the dot-multiplication gives
Replacing each dot product with a unique scalar gives
and these equations can be expressed as the single matrix equation
This matrix equation relates the scalar components of a in the n basis (u,v, and w) with those in the e basis (p, q, and r). Each matrix element cjk is the direction cosine relating nj to ek. The term direction cosine refers to the cosine of the angle between two unit vectors, which is also equal to their dot product. Therefore,
By referring collectively to e1, e2, e3 as the e basis and to n1, n2, n3 as the n basis, the matrix containing all the cjk is known as the "transformation matrix from e to n", or the "rotation matrix from e to n" (because it can be imagined as the "rotation" of a vector from one basis to another), or the "direction cosine matrix from e to n" (because it contains direction cosines). The properties of a rotation matrix are such that its inverse is equal to its transpose. This means that the "rotation matrix from e to n" is the transpose of "rotation matrix from n to e".
The properties of a direction cosine matrix, C are:
- the determinant is unity, |C| = 1;
- the inverse is equal to the transpose;
- the rows and columns are orthogonal unit vectors, therefore their dot products are zero.
The advantage of this method is that a direction cosine matrix can usually be obtained independently by using Euler angles or a quaternion to relate the two vector bases, so the basis conversions can be performed directly, without having to work out all the dot products described above.
By applying several matrix multiplications in succession, any vector can be expressed in any basis so long as the set of direction cosines is known relating the successive bases.
Other dimensions
With the exception of the cross and triple products, the above formulae generalise to two dimensions and higher dimensions. For example, addition generalises to two dimensions as
The cross product does not readily generalise to other dimensions, though the closely related exterior product does, whose result is a bivector. In two dimensions this is simply a pseudoscalar
A seven-dimensional cross product is similar to the cross product in that its result is a vector orthogonal to the two arguments; there is however no natural way of selecting one of the possible such products.
Dot Product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors), and returns a single number. In Euclidean geometry, the dot product of the Cartesian coordinates of two vectors is widely used. It is often called "the" inner product (or rarely projection product) of Euclidean space, even though it is not the only inner product that can be defined on Euclidean space.
Algebraically, the dot product is the sum of the products of the corresponding entries of the two sequences of numbers. Geometrically, it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them. These definitions are equivalent when using Cartesian coordinates. In modern geometry, Euclidean spaces are often defined by using vector spaces. In this case, the dot product is used for defining lengths (the length of a vector is the square root of the dot product of the vector by itself) and angles (the cosine of the angle of two vectors is the quotient of their dot product by the product of their lengths).
The name "dot product" is derived from the centered dot " · ", that is often used to designate this operation; the alternative name "scalar product" emphasizes that the result is a scalar, rather than a vector, as is the case for the vector product in three-dimensional space.
Definition
The dot product may be defined algebraically or geometrically. The geometric definition is based on the notions of angle and distance (magnitude of vectors). The equivalence of these two definitions relies on having a Cartesian coordinate system for Euclidean space.
In modern presentations of Euclidean geometry, the points of space are defined in terms of their Cartesian coordinates, and Euclidean space itself is commonly identified with the real coordinate space Rn. In such a presentation, the notions of length and angles are defined by means of the dot product. The length of a vector is defined as the square root of the dot product of the vector by itself, and the cosine of the (non oriented) angle of two vectors of length one is defined as their dot product. So the equivalence of the two definitions of the dot product is a part of the equivalence of the classical and the modern formulations of Euclidean geometry.
Algebraic definition
The dot product of two vectors = and = is defined as:
where Σ denotes summation and n is the dimension of the vector space. For instance, in three-dimensional space, the dot product of vectors and is:
If vectors are identified with row matrices, the dot product can also be written as a matrix product
where denotes the transpose of .
Expressing the above example in this way, a 1 × 3 matrix (row vector) is multiplied by a 3 × 1 matrix (column vector) to get a 1 × 1 matrix that is identified with its unique entry:
- .
Geometric definition
In Euclidean space, a Euclidean vector is a geometric object that possesses both a magnitude and a direction. A vector can be pictured as an arrow. Its magnitude is its length, and its direction is the direction to which the arrow points. The magnitude of a vector a is denoted by . The dot product of two Euclidean vectors a and b is defined by
where θ is the angle between a and b.
In particular, if the vectors a and b are orthogonal (i.e., their angle is / 2}} or 90°), then , which implies that
At the other extreme, if they are codirectional, then the angle between them is zero with and
This implies that the dot product of a vector a with itself is
which gives
the formula for the Euclidean length of the vector.
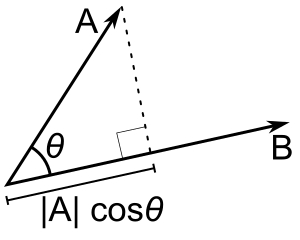
Scalar projection and first properties
The scalar projection (or scalar component) of a Euclidean vector a in the direction of a Euclidean vector b is given by
where θ is the angle between a and b.
In terms of the geometric definition of the dot product, this can be rewritten
where is the unit vector in the direction of b.
The dot product is thus characterized geometrically by
The dot product, defined in this manner, is homogeneous under scaling in each variable, meaning that for any scalar α,
It also satisfies a distributive law, meaning that
These properties may be summarized by saying that the dot product is a bilinear form. Moreover, this bilinear form is positive definite, which means that is never negative, and is zero if and only if —the zero vector.
The dot product is thus equivalent to multiplying the norm (length) of b by the norm of the projection of a over b.
Equivalence of the definitions
If e1, ..., en are the standard basis vectors in Rn, then we may write
The vectors ei are an orthonormal basis, which means that they have unit length and are at right angles to each other. Hence since these vectors have unit length
and since they form right angles with each other, if i ≠ j,
Thus in general, we can say that:
Where δ ij is the Kronecker delta.
Also, by the geometric definition, for any vector ei and a vector a, we note
where ai is the component of vector a in the direction of ei. The last step in the equality can be seen from the figure.
Now applying the distributivity of the geometric version of the dot product gives
which is precisely the algebraic definition of the dot product. So the geometric dot product equals the algebraic dot product.
Properties
The dot product fulfills the following properties if a, b, and c are real vectors and r is a scalar.
- Commutative:
- which follows from the definition (θ is the angle between a and b):
- Distributive over vector addition:
- Bilinear:
- Scalar multiplication:
- Not associative because the dot product between a scalar (a ⋅ b) and a vector (c) is not defined, which means that the expressions involved in the associative property, (a ⋅ b) ⋅ c or a ⋅ (b ⋅ c) are both ill-defined. Note however that the previously mentioned scalar multiplication property is sometimes called the "associative law for scalar and dot product" or one can say that "the dot product is associative with respect to scalar multiplication" because c (a ⋅ b) = (c a) ⋅ b = a ⋅ (c b).
- Orthogonal:
- Two non-zero vectors a and b are orthogonal if and only if a ⋅ b = 0.
- No cancellation:
- Unlike multiplication of ordinary numbers, where if ab = ac, then b always equals c unless a is zero, the dot product does not obey the cancellation law:
- If a ⋅ b = a ⋅ c and a ≠ 0, then we can write: a ⋅ (b − c) = 0 by the distributive law; the result above says this just means that a is perpendicular to (b − c), which still allows (b − c) ≠ 0, and therefore allows b ≠ c.
- Product Rule:
- If a and b are (vector-valued) differentiable functions, then the derivative (denoted by a prime ') of a ⋅ b is given by the rule (a ⋅ b)' = a' ⋅ b + a ⋅ b'.
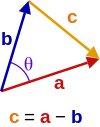
Application to the law of cosines
Given two vectors a and b separated by angle θ (see image right), they form a triangle with a third side = − . The dot product of this with itself is:
which is the law of cosines.
Triple product
There are two ternary operations involving dot product and cross product.
The scalar triple product of three vectors is defined as
Its value is the determinant of the matrix whose columns are the Cartesian coordinates of the three vectors. It is the signed volume of the parallelepiped defined by the three vectors, and is isomorphic to the three-dimensional special case of the exterior product of three vectors.
The vector triple product is defined by
This identity, also known as Lagrange's formula, may be remembered as "ACB minus ABC", keeping in mind which vectors are dotted together. This formula has applications in simplifying vector calculations in physics.
Matrices
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object.
For example,
Without further specifications, matrices represent linear maps, and allow explicit computations in linear algebra. Therefore, the study of matrices is a large part of linear algebra, and most properties and operations of abstract linear algebra can be expressed in terms of matrices. For example, matrix multiplication represents composition of linear maps.
Not all matrices are related to linear algebra. This is, in particular, the case in graph theory, of incidence matrices, and adjacency matrices. This article focuses on matrices related to linear algebra, and, unless otherwise specified, all matrices represent linear maps or may be viewed as such.
Square matrices, matrices with the same number of rows and columns, play a major role in matrix theory. Square matrices of a given dimension form a noncommutative ring, which is one of the most common examples of a noncommutative ring. The determinant of a square matrix is a number associated to the matrix, which is fundamental for the study of a square matrix; for example, a square matrix is invertible if and only if it has a nonzero determinant, and the eigenvalues of a square matrix are the roots of a polynomial determinant.
In geometry, matrices are widely used for specifying and representing geometric transformations (for example rotations) and coordinate changes. In numerical analysis, many computational problems are solved by reducing them to a matrix computation, and this involves often to compute with matrices of huge dimension. Matrices are used in most areas of mathematics and most scientific fields, either directly, or through their use in geometry and numerical analysis.
Definition
A matrix is a rectangular array of numbers (or other mathematical objects), called the entries of the matrix. Matrices are subject to standard operations such as addition and multiplication. Most commonly, a matrix over a field F is a rectangular array of elements of F. A real matrix and a complex matrix are matrices whose entries are respectively real numbers or complex numbers. More general types of entries are discussed below. For instance, this is a real matrix:
The numbers, symbols, or expressions in the matrix are called its entries or its elements. The horizontal and vertical lines of entries in a matrix are called rows and columns, respectively.
Size
The size of a matrix is defined by the number of rows and columns it contains. There is no limit to the numbers of rows and columns a matrix (in the usual sense) can have as long as they are positive integers. A matrix with m rows and n columns is called an m × n matrix, or m-by-n matrix, while m and n are called its dimensions. For example, the matrix A above is a 3 × 2 matrix.
Matrices with a single row are called row vectors, and those with a single column are called column vectors. A matrix with the same number of rows and columns is called a square matrix. A matrix with an infinite number of rows or columns (or both) is called an infinite matrix. In some contexts, such as computer algebra programs, it is useful to consider a matrix with no rows or no columns, called an empty matrix.
| Name | Size | Example | Description |
|---|---|---|---|
| Row vector | 1 × n | A matrix with one row, sometimes used to represent a vector | |
| Column vector | n × 1 | A matrix with one column, sometimes used to represent a vector | |
| Square matrix | n × n | A matrix with the same number of rows and columns, sometimes used to represent a linear transformation from a vector space to itself, such as reflection, rotation, or shearing. |
Notation
Matrices are commonly written in box brackets or parentheses:
The specifics of symbolic matrix notation vary widely, with some prevailing trends. Matrices are usually symbolized using upper-case letters (such as A in the examples above), while the corresponding lower-case letters, with two subscript indices (e.g., a11, or a1,1), represent the entries. In addition to using upper-case letters to symbolize matrices, many authors use a special typographical style, commonly boldface upright (non-italic), to further distinguish matrices from other mathematical objects. An alternative notation involves the use of a double-underline with the variable name, with or without boldface style (as in the case of ).
The entry in the i-th row and j-th column of a matrix A is sometimes referred to as the i,j, (i,j), or (i,j)th entry of the matrix, and most commonly denoted as ai,j, or aij. Alternative notations for that entry are A[i,j] or Ai,j. For example, the (1,3) entry of the following matrix A is 5 (also denoted a13, a1,3, A[1,3] or A1,3):
Sometimes, the entries of a matrix can be defined by a formula such as ai,j = f(i, j). For example, each of the entries of the following matrix A is determined by the formula aij = i − j.
In this case, the matrix itself is sometimes defined by that formula, within square brackets or double parentheses. For example, the matrix above is defined as A = [i−j], or A = ((i−j)). If matrix size is m × n, the above-mentioned formula f(i, j) is valid for any i = 1, ..., m and any j = 1, ..., n. This can be either specified separately, or indicated using m × n as a subscript. For instance, the matrix A above is 3 × 4, and can be defined as A = [i − j] (i = 1, 2, 3; j = 1, ..., 4), or A = [i − j]3×4.
Some programming languages utilize doubly subscripted arrays (or arrays of arrays) to represent an m-×-n matrix. Some programming languages start the numbering of array indexes at zero, in which case the entries of an m-by-n matrix are indexed by 0 ≤ i ≤ m − 1 and 0 ≤ j ≤ n − 1. This article follows the more common convention in mathematical writing where enumeration starts from 1.
An asterisk is occasionally used to refer to whole rows or columns in a matrix. For example, ai,∗ refers to the ith row of A, and a∗,j refers to the jth column of A.
The set of all m-by-n real matrices is often denoted or The set of all m-by-n matrices matrices over another field or over a ring R, is similarly denoted or If m = n, that is, in the case of square matrices, one does not repeat the dimension: or Often, is used in place of
Basic operations
There are a number of basic operations that can be applied to modify matrices, called matrix addition, scalar multiplication, transposition, matrix multiplication, row operations, and submatrix.
Addition, scalar multiplication, and transposition
| Operation | Definition | Example |
|---|---|---|
| Addition | The sum A+B of two m-by-n matrices A and B is calculated entrywise:
|
|
| Scalar multiplication | The product cA of a number c (also called a scalar in the parlance of abstract algebra) and a matrix A is computed by multiplying every entry of A by c:
This operation is called scalar multiplication, but its result is not named "scalar product" to avoid confusion, since "scalar product" is sometimes used as a synonym for "inner product". |
|
| Transposition | The transpose of an m-by-n matrix A is the n-by-m matrix AT (also denoted Atr or tA) formed by turning rows into columns and vice versa:
|
Familiar properties of numbers extend to these operations of matrices: for example, addition is commutative, that is, the matrix sum does not depend on the order of the summands: A + B = B + A. The transpose is compatible with addition and scalar multiplication, as expressed by (cA)T = c(AT) and (A + B)T = AT + BT. Finally, (AT)T = A.
Matrix multiplication
Multiplication of two matrices is defined if and only if the number of columns of the left matrix is the same as the number of rows of the right matrix. If A is an m-by-n matrix and B is an n-by-p matrix, then their matrix product AB is the m-by-p matrix whose entries are given by dot product of the corresponding row of A and the corresponding column of B:
where 1 ≤ i ≤ m and 1 ≤ j ≤ p. For example, the underlined entry 2340 in the product is calculated as (2 × 1000) + (3 × 100) + (4 × 10) = 2340:
Matrix multiplication satisfies the rules (AB)C = A(BC) (associativity), and (A + B)C = AC + BC as well as C(A + B) = CA + CB (left and right distributivity), whenever the size of the matrices is such that the various products are defined. The product AB may be defined without BA being defined, namely if A and B are m-by-n and n-by-k matrices, respectively, and m ≠ k. Even if both products are defined, they generally need not be equal, that is:
- AB ≠ BA,
In other words, matrix multiplication is not commutative, in marked contrast to (rational, real, or complex) numbers, whose product is independent of the order of the factors. An example of two matrices not commuting with each other is:
whereas
Besides the ordinary matrix multiplication just described, other less frequently used operations on matrices that can be considered forms of multiplication also exist, such as the Hadamard product and the Kronecker product. They arise in solving matrix equations such as the Sylvester equation.
Row operations
There are three types of row operations:
- row addition, that is adding a row to another.
- row multiplication, that is multiplying all entries of a row by a non-zero constant;
- row switching, that is interchanging two rows of a matrix;
These operations are used in several ways, including solving linear equations and finding matrix inverses.
Submatrix
A submatrix of a matrix is obtained by deleting any collection of rows and/or columns. For example, from the following 3-by-4 matrix, we can construct a 2-by-3 submatrix by removing row 3 and column 2:
The minors and cofactors of a matrix are found by computing the determinant of certain submatrices.
A principal submatrix is a square submatrix obtained by removing certain rows and columns. The definition varies from author to author. According to some authors, a principal submatrix is a submatrix in which the set of row indices that remain is the same as the set of column indices that remain. Other authors define a principal submatrix as one in which the first k rows and columns, for some number k, are the ones that remain; this type of submatrix has also been called a leading principal submatrix.
Linear equations
Matrices can be used to compactly write and work with multiple linear equations, that is, systems of linear equations. For example, if A is an m-by-n matrix, x designates a column vector (that is, n×1-matrix) of n variables x1, x2, ..., xn, and b is an m×1-column vector, then the matrix equation
is equivalent to the system of linear equations
Using matrices, this can be solved more compactly than would be possible by writing out all the equations separately. If n = m and the equations are independent, then this can be done by writing
where A−1 is the inverse matrix of A. If A has no inverse, solutions—if any—can be found using its generalized inverse.
Linear transformations
Matrices and matrix multiplication reveal their essential features when related to linear transformations, also known as linear maps. A real m-by-n matrix A gives rise to a linear transformation Rn → Rm mapping each vector x in Rn to the (matrix) product Ax, which is a vector in Rm. Conversely, each linear transformation f: Rn → Rm arises from a unique m-by-n matrix A: explicitly, the (i, j)-entry of A is the ith coordinate of f(ej), where ej = (0,...,0,1,0,...,0) is the unit vector with 1 in the jth position and 0 elsewhere. The matrix A is said to represent the linear map f, and A is called the transformation matrix of f.
For example, the 2×2 matrix
can be viewed as the transform of the unit square into a parallelogram with vertices at (0, 0), (a, b), (a + c, b + d), and (c, d). The parallelogram pictured at the right is obtained by multiplying A with each of the column vectors , and in turn. These vectors define the vertices of the unit square.
The following table shows several 2×2 real matrices with the associated linear maps of R2. The blue original is mapped to the green grid and shapes. The origin (0,0) is marked with a black point.
| Horizontal shear with m = 1.25. |
Reflection through the vertical axis | Squeeze mapping with r = 3/2 |
Scaling by a factor of 3/2 |
Rotation by /6 = 30° |

|

|

|

|

|
Under the 1-to-1 correspondence between matrices and linear maps, matrix multiplication corresponds to composition of maps: if a k-by-m matrix B represents another linear map g: Rm → Rk, then the composition g ∘ f is represented by BA since
- (g ∘ f)(x) = g(f(x)) = g(Ax) = B(Ax) = (BA)x.
The last equality follows from the above-mentioned associativity of matrix multiplication.
The rank of a matrix A is the maximum number of linearly independent row vectors of the matrix, which is the same as the maximum number of linearly independent column vectors. Equivalently it is the dimension of the image of the linear map represented by A. The rank–nullity theorem states that the dimension of the kernel of a matrix plus the rank equals the number of columns of the matrix.
Square matrix
A square matrix is a matrix with the same number of rows and columns. An n-by-n matrix is known as a square matrix of order n. Any two square matrices of the same order can be added and multiplied. The entries aii form the main diagonal of a square matrix. They lie on the imaginary line that runs from the top left corner to the bottom right corner of the matrix.
Main types
Name Example with n = 3 Diagonal matrix Lower triangular matrix Upper triangular matrix
Diagonal and triangular matrix
If all entries of A below the main diagonal are zero, A is called an upper triangular matrix. Similarly if all entries of A above the main diagonal are zero, A is called a lower triangular matrix. If all entries outside the main diagonal are zero, A is called a diagonal matrix.
Identity matrix
The identity matrix In of size n is the n-by-n matrix in which all the elements on the main diagonal are equal to 1 and all other elements are equal to 0, for example,
It is a square matrix of order n, and also a special kind of diagonal matrix. It is called an identity matrix because multiplication with it leaves a matrix unchanged:
- AIn = ImA = A for any m-by-n matrix A.
A nonzero scalar multiple of an identity matrix is called a scalar matrix. If the matrix entries come from a field, the scalar matrices form a group, under matrix multiplication, that is isomorphic to the multiplicative group of nonzero elements of the field.
Symmetric or skew-symmetric matrix
A square matrix A that is equal to its transpose, that is, A = AT, is a symmetric matrix. If instead, A is equal to the negative of its transpose, that is, A = −AT, then A is a skew-symmetric matrix. In complex matrices, symmetry is often replaced by the concept of Hermitian matrices, which satisfy A∗ = A, where the star or asterisk denotes the conjugate transpose of the matrix, that is, the transpose of the complex conjugate of A.
By the spectral theorem, real symmetric matrices and complex Hermitian matrices have an eigenbasis; that is, every vector is expressible as a linear combination of eigenvectors. In both cases, all eigenvalues are real. This theorem can be generalized to infinite-dimensional situations related to matrices with infinitely many rows and columns.
Invertible matrix and its inverse
A square matrix A is called invertible or non-singular if there exists a matrix B such that
- AB = BA = In ,
where In is the n×n identity matrix with 1s on the main diagonal and 0s elsewhere. If B exists, it is unique and is called the inverse matrix of A, denoted A−1.
Definite matrix
| Positive definite matrix | Indefinite matrix |
|---|---|
| Q(x, y) = x2 + y2 | Q(x, y) = x2 - y2 |
 Points such that Q(x,y)=1 (Ellipse). |
 Points such that Q(x,y)=1 (Hyperbola). |
A symmetric real matrix A is called positive-definite if the associated quadratic form
- f(x) = xTA x
has a positive value for every nonzero vector x in Rn. If f(x) only yields negative values then A is negative-definite; if f does produce both negative and positive values then A is indefinite. If the quadratic form f yields only non-negative values (positive or zero), the symmetric matrix is called positive-semidefinite (or if only non-positive values, then negative-semidefinite); hence the matrix is indefinite precisely when it is neither positive-semidefinite nor negative-semidefinite.
A symmetric matrix is positive-definite if and only if all its eigenvalues are positive, that is, the matrix is positive-semidefinite and it is invertible. The table at the right shows two possibilities for 2-by-2 matrices.
Allowing as input two different vectors instead yields the bilinear form associated to A:
- BA (x, y) = xTAy.
In the case of complex matrices, the same terminology and result apply, with symmetric matrix, quadratic form, bilinear form, and transpose xT replaced respectively by Hermitian matrix, Hermitian form, sesquilinear form, and conjugate transpose xH.
Orthogonal matrix
An orthogonal matrix is a square matrix with real entries whose columns and rows are orthogonal unit vectors (that is, orthonormal vectors). Equivalently, a matrix A is orthogonal if its transpose is equal to its inverse:
which entails
where In is the identity matrix of size n.
An orthogonal matrix A is necessarily invertible (with inverse A-1 = AT), unitary (A-1 = A*), and normal A*A = AA*). The determinant of any orthogonal matrix is either +1 or −1. A special orthogonal matrix is an orthogonal matrix with determinant +1. As a linear transformation, every orthogonal matrix with determinant +1 is a pure rotation without reflection, i.e., the transformation preserves the orientation of the transformed structure, while every orthogonal matrix with determinant -1 reverses the orientation, i.e., is a composition of a pure reflection and a (possibly null) rotation. The identity matrices have determinant 1, and are pure rotations by an angle zero.
The complex analogue of an orthogonal matrix is a unitary matrix.
Main operations
Trace
The trace, tr(A) of a square matrix A is the sum of its diagonal entries. While matrix multiplication is not commutative as mentioned above, the trace of the product of two matrices is independent of the order of the factors:
- tr(AB) = tr(BA).
This is immediate from the definition of matrix multiplication:
It follows that the trace of the product of more than two matrices is independent of cyclic permutations of the matrices, however this does not in general apply for arbitrary permutations (for example, tr(ABC) ≠ tr(BAC), in general). Also, the trace of a matrix is equal to that of its transpose, that is,
- tr(A) = tr(AT).
Determinant
The determinant of a square matrix A (denoted det(A) or |A|) is a number encoding certain properties of the matrix. A matrix is invertible if and only if its determinant is nonzero. Its absolute value equals the area (in R2) or volume (in R3) of the image of the unit square (or cube), while its sign corresponds to the orientation of the corresponding linear map: the determinant is positive if and only if the orientation is preserved.
The determinant of 2-by-2 matrices is given by
The determinant of 3-by-3 matrices involves 6 terms (rule of Sarrus). The more lengthy Leibniz formula generalises these two formulae to all dimensions.
The determinant of a product of square matrices equals the product of their determinants:
- det(AB) = det(A) · det(B).
Adding a multiple of any row to another row, or a multiple of any column to another column does not change the determinant. Interchanging two rows or two columns affects the determinant by multiplying it by −1. Using these operations, any matrix can be transformed to a lower (or upper) triangular matrix, and for such matrices, the determinant equals the product of the entries on the main diagonal; this provides a method to calculate the determinant of any matrix. Finally, the Laplace expansion expresses the determinant in terms of minors, that is, determinants of smaller matrices. This expansion can be used for a recursive definition of determinants (taking as starting case the determinant of a 1-by-1 matrix, which is its unique entry, or even the determinant of a 0-by-0 matrix, which is 1), that can be seen to be equivalent to the Leibniz formula. Determinants can be used to solve linear systems using Cramer's rule, where the division of the determinants of two related square matrices equates to the value of each of the system's variables.
Eigenvalues and eigenvectors
A number λ and a non-zero vector v satisfying
are called an eigenvalue and an eigenvector of A, respectively. The number λ is an eigenvalue of an n×n-matrix A if and only if A−λIn is not invertible, which is equivalent to
The polynomial pA in an indeterminate X given by evaluation of the determinant det(XIn−A) is called the characteristic polynomial of A. It is a monic polynomial of degree n. Therefore the polynomial equation pA(λ) = 0 has at most n different solutions, that is, eigenvalues of the matrix. They may be complex even if the entries of A are real. According to the Cayley–Hamilton theorem, pA(A) = 0, that is, the result of substituting the matrix itself into its own characteristic polynomial yields the zero matrix.
Gauss-Jordan Elimination
In mathematics, Gaussian elimination, also known as row reduction, is an algorithm for solving systems of linear equations. It consists of a sequence of operations performed on the corresponding matrix of coefficients. This method can also be used to compute the rank of a matrix, the determinant of a square matrix, and the inverse of an invertible matrix. The method is named after Carl Friedrich Gauss (1777–1855) although some special cases of the method—albeit presented without proof—were known to Chinese mathematicians as early as circa 179 CE.
To perform row reduction on a matrix, one uses a sequence of elementary row operations to modify the matrix until the lower left-hand corner of the matrix is filled with zeros, as much as possible. There are three types of elementary row operations:
- Swapping two rows,
- Multiplying a row by a nonzero number,
- Adding a multiple of one row to another row. (subtraction can be achieved by multiplying one row with -1 and adding the result to another row)
Using these operations, a matrix can always be transformed into an upper triangular matrix, and in fact one that is in row echelon form. Once all of the leading coefficients (the leftmost nonzero entry in each row) are 1, and every column containing a leading coefficient has zeros elsewhere, the matrix is said to be in reduced row echelon form. This final form is unique; in other words, it is independent of the sequence of row operations used. For example, in the following sequence of row operations (where two elementary operations on different rows are done at the first and third steps), the third and fourth matrices are the ones in row echelon form, and the final matrix is the unique reduced row echelon form.
Using row operations to convert a matrix into reduced row echelon form is sometimes called Gauss–Jordan elimination. In this case, the term Gaussian elimination refers to the process until it has reached its upper triangular, or (unreduced) row echelon form. For computational reasons, when solving systems of linear equations, it is sometimes preferable to stop row operations before the matrix is completely reduced.
Definitions and example of algorithm
The process of row reduction makes use of elementary row operations, and can be divided into two parts. The first part (sometimes called forward elimination) reduces a given system to row echelon form, from which one can tell whether there are no solutions, a unique solution, or infinitely many solutions. The second part (sometimes called back substitution) continues to use row operations until the solution is found; in other words, it puts the matrix into reduced row echelon form.
Another point of view, which turns out to be very useful to analyze the algorithm, is that row reduction produces a matrix decomposition of the original matrix. The elementary row operations may be viewed as the multiplication on the left of the original matrix by elementary matrices. Alternatively, a sequence of elementary operations that reduces a single row may be viewed as multiplication by a Frobenius matrix. Then the first part of the algorithm computes an LU decomposition, while the second part writes the original matrix as the product of a uniquely determined invertible matrix and a uniquely determined reduced row echelon matrix.
Row operations
There are three types of elementary row operations which may be performed on the rows of a matrix:
- Swap the positions of two rows.
- Multiply a row by a non-zero scalar.
- Add to one row a scalar multiple of another.
If the matrix is associated to a system of linear equations, then these operations do not change the solution set. Therefore, if one's goal is to solve a system of linear equations, then using these row operations could make the problem easier.
Echelon form
For each row in a matrix, if the row does not consist of only zeros, then the leftmost nonzero entry is called the leading coefficient (or pivot) of that row. So if two leading coefficients are in the same column, then a row operation of type 3 could be used to make one of those coefficients zero. Then by using the row swapping operation, one can always order the rows so that for every non-zero row, the leading coefficient is to the right of the leading coefficient of the row above. If this is the case, then matrix is said to be in row echelon form. So the lower left part of the matrix contains only zeros, and all of the zero rows are below the non-zero rows. The word "echelon" is used here because one can roughly think of the rows being ranked by their size, with the largest being at the top and the smallest being at the bottom.
For example, the following matrix is in row echelon form, and its leading coefficients are shown in red:
It is in echelon form because the zero row is at the bottom, and the leading coefficient of the second row (in the third column), is to the right of the leading coefficient of the first row (in the second column).
A matrix is said to be in reduced row echelon form if furthermore all of the leading coefficients are equal to 1 (which can be achieved by using the elementary row operation of type 2), and in every column containing a leading coefficient, all of the other entries in that column are zero (which can be achieved by using elementary row operations of type 3).
Example of the algorithm
Suppose the goal is to find and describe the set of solutions to the following system of linear equations:
The table below is the row reduction process applied simultaneously to the system of equations and its associated augmented matrix. In practice, one does not usually deal with the systems in terms of equations, but instead makes use of the augmented matrix, which is more suitable for computer manipulations. The row reduction procedure may be summarized as follows: eliminate x from all equations below L1, and then eliminate y from all equations below L2. This will put the system into triangular form. Then, using back-substitution, each unknown can be solved for.
System of equations Row operations Augmented matrix The matrix is now in echelon form (also called triangular form)
The second column describes which row operations have just been performed. So for the first step, the x is eliminated from L2 by adding L1 to L2. Next, x is eliminated from L3 by adding L1 to L3. These row operations are labelled in the table as
Once y is also eliminated from the third row, the result is a system of linear equations in triangular form, and so the first part of the algorithm is complete. From a computational point of view, it is faster to solve the variables in reverse order, a process known as back-substitution. One sees the solution is z = −1}}, y = 3, and x = 2. So there is a unique solution to the original system of equations.
Instead of stopping once the matrix is in echelon form, one could continue until the matrix is in reduced row echelon form, as it is done in the table. The process of row reducing until the matrix is reduced is sometimes referred to as Gauss–Jordan elimination, to distinguish it from stopping after reaching echelon form.
Applications
Historically, the first application of the row reduction method is for solving systems of linear equations. Here are some other important applications of the algorithm.
Computing determinants
To explain how Gaussian elimination allows the computation of the determinant of a square matrix, we have to recall how the elementary row operations change the determinant:
- Swapping two rows multiplies the determinant by −1
- Multiplying a row by a nonzero scalar multiplies the determinant by the same scalar
- Adding to one row a scalar multiple of another does not change the determinant.
If Gaussian elimination applied to a square matrix A produces a row echelon matrix B, let d be the product of the scalars by which the determinant has been multiplied, using the above rules. Then the determinant of A is the quotient by d of the product of the elements of the diagonal of B:
Computationally, for an n × n matrix, this method needs only O(n3) arithmetic operations, while using Leibniz formula for determinants requires O(n!) operations (number of summands in the formula), and recursive Laplace expansion requires O(2n) operations (number of sub-determinants to compute, if none is computed twice). Even on the fastest computers, these two methods are impractical or almost impracticable for n above 20.
Finding the inverse of a matrix
A variant of Gaussian elimination called Gauss–Jordan elimination can be used for finding the inverse of a matrix, if it exists. If A is an n × n square matrix, then one can use row reduction to compute its inverse matrix, if it exists. First, the n × n identity matrix is augmented to the right of A, forming an n × 2n block matrix [A | I]. Now through application of elementary row operations, find the reduced echelon form of this n × 2n matrix. The matrix A is invertible if and only if the left block can be reduced to the identity matrix I; in this case the right block of the final matrix is A−1. If the algorithm is unable to reduce the left block to I, then A is not invertible.
For example, consider the following matrix:
To find the inverse of this matrix, one takes the following matrix augmented by the identity and row-reduces it as a 3 × 6 matrix:
By performing row operations, one can check that the reduced row echelon form of this augmented matrix is
One can think of each row operation as the left product by an elementary matrix. Denoting by B the product of these elementary matrices, we showed, on the left, that BA = I, and therefore, B = A−1. On the right, we kept a record of BI = B, which we know is the inverse desired. This procedure for finding the inverse works for square matrices of any size.
Computing ranks and bases
The Gaussian elimination algorithm can be applied to any m × n matrix A. In this way, for example, some 6 × 9 matrices can be transformed to a matrix that has a row echelon form like
where the stars are arbitrary entries, and a, b, c, d, e are nonzero entries. This echelon matrix T contains a wealth of information about A: the rank of A is 5, since there are 5 nonzero rows in T; the vector space spanned by the columns of A has a basis consisting of its columns 1, 3, 4, 7 and 9 (the columns with a, b, c, d, e in T), and the stars show how the other columns of A can be written as linear combinations of the basis columns. This is a consequence of the distributivity of the dot product in the expression of a linear map as a matrix.
All of this applies also to the reduced row echelon form, which is a particular row echelon format.
Licensing
Content obtained and/or adapted from:
- Euclidean vector, Wikipedia under a CC BY-SA license
- Dot product, Wikipedia under a CC BY-SA license
- Matrix (mathematics), Wikipedia under a CC BY-SA license
- Gaussian elimination, Wikipedia under a CC BY-SA license


















![{\displaystyle \mathbf {a} ={\begin{bmatrix}a_{1}\\a_{2}\\a_{3}\\\end{bmatrix}}=[a_{1}\ a_{2}\ a_{3}]^{\operatorname {T} }.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a4d592431150c7ec8a51217d87dae2ed1224df2)
















































![{\displaystyle \mathbf {\color {red}[a_{1},a_{2},\ldots ,a_{n}} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b892e14b44bfe1ad406723b06f0cdb6e4de27c88)

![{\displaystyle \mathbf {\color {blue}[b_{1},b_{2},\ldots ,b_{n}} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/013521bc1e25b5951156021ae4afd225786ff65b)

![{\displaystyle \mathbf {\color {red}[1,3,-5]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d37c8fb0bfb1ab79a244930132b0720d9abf8096)
![{\displaystyle \mathbf {\color {blue}[4,-2,-1]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4aea7b92e37d28608f0bb363a0215a2d9a49b68b)
![{\displaystyle {\begin{aligned}\ [{\color {red}1,3,-5}]\cdot [{\color {blue}4,-2,-1}]&=({\color {red}1}\times {\color {blue}4})+({\color {red}3}\times {\color {blue}-2})+({\color {red}-5}\times {\color {blue}-1})\\&=4-6+5\\&=3\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be560d2c22a074c7711ae946954725d31ec77928)























![{\displaystyle {\begin{aligned}\mathbf {a} &=[a_{1},\dots ,a_{n}]=\sum _{i}a_{i}\mathbf {e} _{i}\\\mathbf {b} &=[b_{1},\dots ,b_{n}]=\sum _{i}b_{i}\mathbf {e} _{i}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b154ac2bb09512c81d917db83c273055c093571f)




































![{\displaystyle [\mathbf {AB} ]_{i,j}=a_{i,1}b_{1,j}+a_{i,2}b_{2,j}+\cdots +a_{i,n}b_{n,j}=\sum _{r=1}^{n}a_{i,r}b_{r,j},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c903c2c14d249005ce9ebaa47a8d6c6710c1c29e)


































![{\displaystyle \left[{\begin{array}{rrr|r}2&1&-1&8\\-3&-1&2&-11\\-2&1&2&-3\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/143d91265d57a1d2bd91ef95aec9f2e466ba411b)


![{\displaystyle \left[{\begin{array}{rrr|r}2&1&-1&8\\0&{\frac {1}{2}}&{\frac {1}{2}}&1\\0&2&1&5\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a368395ec0a81beb81a1bc835a8b104c1d5f8d93)


![{\displaystyle \left[{\begin{array}{rrr|r}2&1&-1&8\\0&{\frac {1}{2}}&{\frac {1}{2}}&1\\0&0&-1&1\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c242ea95eafb698feb0e71360d1195f6be661fd9)


![{\displaystyle \left[{\begin{array}{rrr|r}2&1&0&7\\0&{\frac {1}{2}}&0&{\frac {3}{2}}\\0&0&-1&1\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cce134ae20452ed7378af60bec807fc56bd4038)


![{\displaystyle \left[{\begin{array}{rrr|r}2&1&0&7\\0&1&0&3\\0&0&1&-1\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33afffad90133de42a6ab976ffe3e728ffe5a128)


![{\displaystyle \left[{\begin{array}{rrr|r}1&0&0&2\\0&1&0&3\\0&0&1&-1\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/158d23387edac419ba2e00a3b6bcf0f400779f2c)




![{\displaystyle [A|I]=\left[{\begin{array}{ccc|ccc}2&-1&0&1&0&0\\-1&2&-1&0&1&0\\0&-1&2&0&0&1\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef2445b659c70c0d78db9f3aca137bc6d3b2dfed)
![{\displaystyle [I|B]=\left[{\begin{array}{rrr|rrr}1&0&0&{\frac {3}{4}}&{\frac {1}{2}}&{\frac {1}{4}}\\0&1&0&{\frac {1}{2}}&1&{\frac {1}{2}}\\0&0&1&{\frac {1}{4}}&{\frac {1}{2}}&{\frac {3}{4}}\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0e25bb831e84d53db3dc956eea13d0304e16984)
