Suppose we are given a function and would like to determine the area underneath its graph over an interval. We could guess, but how could we figure out the exact area? Below, using a few clever ideas, we actually define such an area and show that by using what is called the definite integral we can indeed determine the exact area underneath a curve.
Introduction

Figure 1: Approximation of the area under the curve

from

to

.

Figure 2: Rectangle approximating the area under the curve from

to

with sample point

.
The rough idea of defining the area under the graph of  is to approximate this area with a finite number of rectangles. Since we can easily work out the area of the rectangles, we get an estimate of the area under the graph. If we use a larger number of smaller-sized rectangles we expect greater accuracy with respect to the area under the curve and hence a better approximation. Somehow, it seems that we could use our old friend from differentiation, the limit, and "approach" an infinite number of rectangles to get the exact area. Let's look at such an idea more closely.
is to approximate this area with a finite number of rectangles. Since we can easily work out the area of the rectangles, we get an estimate of the area under the graph. If we use a larger number of smaller-sized rectangles we expect greater accuracy with respect to the area under the curve and hence a better approximation. Somehow, it seems that we could use our old friend from differentiation, the limit, and "approach" an infinite number of rectangles to get the exact area. Let's look at such an idea more closely.
Suppose we have a function  that is positive on the interval
that is positive on the interval ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) and we want to find the area
and we want to find the area  under
under  between
between  and
and  . Let's pick an integer
. Let's pick an integer  and divide the interval into
and divide the interval into  subintervals of equal width (see Figure 1). As the interval
subintervals of equal width (see Figure 1). As the interval ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) has width
has width  , each subinterval has width
, each subinterval has width  . We denote the endpoints of the subintervals by
. We denote the endpoints of the subintervals by  . This gives us
. This gives us

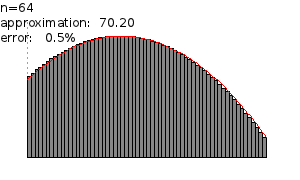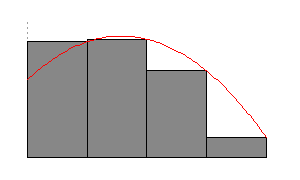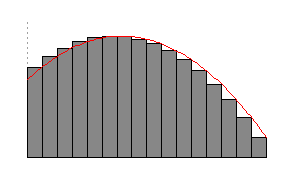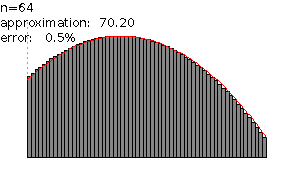
Figure 3: Riemann sums with an increasing number of subdivisions yielding better approximations.
Now for each  pick a sample point
pick a sample point  in the interval
in the interval ![{\displaystyle [x_{i-1},x_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09cb12a889d47020c8ce7046a2eb60785e00c0b6) and consider the rectangle of height
and consider the rectangle of height  and width
and width  (see Figure 2). The area of this rectangle is
(see Figure 2). The area of this rectangle is  . By adding up the area of all the rectangles for
. By adding up the area of all the rectangles for  we get that the area
we get that the area  is approximated by
is approximated by

A more convenient way to write this is with summation notation.

For each number  we get a different approximation. As
we get a different approximation. As  gets larger the width of the rectangles gets smaller which yields a better approximation (see Figure 3). In the limit of
gets larger the width of the rectangles gets smaller which yields a better approximation (see Figure 3). In the limit of  as
as  tends to infinity we get the area
tends to infinity we get the area  .
.
Definition of the Definite Integral
Suppose  is a continuous function on
is a continuous function on ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) and
and  . Then the definite integral of
. Then the definite integral of  between
between  and
and  is
is

where  are any sample points in the interval
are any sample points in the interval ![{\displaystyle [x_{i-1},x_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09cb12a889d47020c8ce7046a2eb60785e00c0b6) and
and  for
for  .
.
It is a fact that if  is continuous on
is continuous on ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) then this limit always exists and does not depend on the choice of the points
then this limit always exists and does not depend on the choice of the points ![{\displaystyle x_{i}^{*}\in [x_{i-1},x_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dafeab86f1179399f11208ee27a15c76434aed3d) . For instance they may be evenly spaced, or distributed ambiguously throughout the interval. The proof of this is technical and is beyond the scope of this section.
. For instance they may be evenly spaced, or distributed ambiguously throughout the interval. The proof of this is technical and is beyond the scope of this section.
Notation
When considering the expression,  (read "the integral from
(read "the integral from  to
to  of the
of the  of
of 
 "), the function
"), the function  is called the integrand and the interval
is called the integrand and the interval ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) is the interval of integration. Also
is the interval of integration. Also  is called the lower limit and
is called the lower limit and  the upper limit of integration.
the upper limit of integration.

Figure 4: The integral gives the signed area under the graph.
One important feature of this definition is that we also allow functions which take negative values. If  for all
for all  then
then  so
so  . So the definite integral of
. So the definite integral of  will be strictly negative. More generally if
will be strictly negative. More generally if  takes on both positive and negative values then
takes on both positive and negative values then  will be the area under the positive part of the graph of
will be the area under the positive part of the graph of  minus the area above the graph of the negative part of the graph (see Figure 4). For this reason we say that
minus the area above the graph of the negative part of the graph (see Figure 4). For this reason we say that  is the signed area under the graph.
is the signed area under the graph.
Independence of Variable
It is important to notice that the variable  did not play an important role in the definition of the integral. In fact we can replace it with any other letter, so the following are all equal:
did not play an important role in the definition of the integral. In fact we can replace it with any other letter, so the following are all equal:

Each of these is the signed area under the graph of  between
between  and
and  . Such a variable is often referred to as a dummy variable or a bound variable.
. Such a variable is often referred to as a dummy variable or a bound variable.
Left and Right Handed Riemann Sums

Figure 5: Right-handed Riemann sum

Figure 6: Left-handed Riemann sum
The following methods are sometimes referred to as L-RAM and R-RAM, RAM standing for "Rectangular Approximation Method."
We could have decided to choose all our sample points  to be on the right hand side of the interval
to be on the right hand side of the interval ![{\displaystyle [x_{i-1},x_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09cb12a889d47020c8ce7046a2eb60785e00c0b6) (see Figure 5). Then
(see Figure 5). Then  for all
for all  and the approximation that we called
and the approximation that we called  for the area becomes
for the area becomes

This is called the right-handed Riemann sum, and the integral is the limit

Alternatively we could have taken each sample point on the left hand side of the interval. In this case  (see Figure 6) and the approximation becomes
(see Figure 6) and the approximation becomes

Then the integral of  is
is

The key point is that, as long as  is continuous, these two definitions give the same answer for the integral.
is continuous, these two definitions give the same answer for the integral.
Examples
Example 1
In this example we will calculate the area under the curve given by the graph of  for
for  between 0 and 1. First we fix an integer
between 0 and 1. First we fix an integer  and divide the interval
and divide the interval ![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d) into
into  subintervals of equal width. So each subinterval has width
subintervals of equal width. So each subinterval has width

To calculate the integral we will use the right-handed Riemann sum. (We could have used the left-handed sum instead, and this would give the same answer in the end). For the right-handed sum the sample points are

Notice that  . Putting this into the formula for the approximation,
. Putting this into the formula for the approximation,

Now we use the formula

to get

To calculate the integral of  between
between  and
and  we take the limit as
we take the limit as  tends to infinity,
tends to infinity,

Example 2
Next we show how to find the integral of the function  between
between  and
and  . This time the interval
. This time the interval ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) has width
has width  so
so

Once again we will use the right-handed Riemann sum. So the sample points we choose are

Thus

|

|
|
|

|
|
|

|
|
|

|
We have to calculate each piece on the right hand side of this equation. For the first two,


For the third sum we have to use a formula

to get

Putting this together

Taking the limit as  tend to infinity gives
tend to infinity gives

|

|
|
|

|
|
|

|
|
|

|
Basic Properties of the Integral
From the definition of the integral we can deduce some basic properties. For all the following rules, suppose that  and
and  are continuous on
are continuous on ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) .
.
The Constant Rule
Constant Rule: 
When  is positive, the height of the function
is positive, the height of the function  at a point
at a point  is
is  times the height of the function
times the height of the function  . So the area under
. So the area under  between
between  and
and  is
is  times the area under
times the area under  . We can also give a proof using the definition of the integral, using the constant rule for limits,
. We can also give a proof using the definition of the integral, using the constant rule for limits,

Example
We saw in the previous section that

Using the constant rule we can use this to calculate that
 ,
, .
.
Example
We saw in the previous section that

We can use this and the constant rule to calculate that

There is a special case of this rule used for integrating constants:
If  is constant then
is constant then 
When  and
and  this integral is the area of a rectangle of height
this integral is the area of a rectangle of height  and width
and width  which equals
which equals  .
.
Example



The addition and subtraction rule
Addition and Subtraction Rules of Integration:


As with the constant rule, the addition rule follows from the addition rule for limits:

|

|
|
|

|
|
|

|
The subtraction rule can be proved in a similar way.
Example
From above  and
and  so
so


Example

The Comparison Rule

Figure 7: Bounding the area under

on
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
Comparison Rule:
- Suppose
 for all
for all ![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce) . Then
. Then

- Suppose
 for all
for all ![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce) . Then
. Then

- Suppose
 for all
for all ![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce) . Then
. Then

If  then each of the rectangles in the Riemann sum to calculate the integral of
then each of the rectangles in the Riemann sum to calculate the integral of  will be above the
will be above the  axis, so the area will be non-negative. If
axis, so the area will be non-negative. If  then
then  and by the first property we get the second property. Finally if
and by the first property we get the second property. Finally if  then the area under the graph of
then the area under the graph of  will be greater than the area of rectangle with height
will be greater than the area of rectangle with height  and less than the area of the rectangle with height
and less than the area of the rectangle with height  (see Figure 7). So
(see Figure 7). So

Linearity with respect to endpoints
Additivity with respect to endpoints:
Suppose  . Then
. Then

Again suppose that  is positive. Then this property should be interpreted as saying that the area under the graph of
is positive. Then this property should be interpreted as saying that the area under the graph of  between
between  and
and  is the area between
is the area between  and
and  plus the area between
plus the area between  and
and  (see Figure 8).
(see Figure 8).

Figure 8: Illustration of the property of additivity with respect to endpoints
{{Calculus/Def|text= Extension of Additivity with respect to limits of integration
When  we have that
we have that  so
so

Also in defining the integral we assumed that  . But the definition makes sense even when
. But the definition makes sense even when  , in which case
, in which case  has changed sign. This gives
has changed sign. This gives

With these definitions,

whatever the order of  .
.
Even and odd functions
Recall that a function  is called odd if it satisfies
is called odd if it satisfies  and is called even if
and is called even if  .
.
Suppose  is a continuous odd function. Then for any
is a continuous odd function. Then for any  ,
,

If  is a continuous even function then for any
is a continuous even function then for any  ,
,

Suppose  is an odd function and consider first just the integral from
is an odd function and consider first just the integral from  to
to  . We make the substitution
. We make the substitution  so
so  . Notice that if
. Notice that if  then
then  and if
and if  then
then  . Hence
. Hence
 .
.
Now as  is odd,
is odd,  so the integral becomes
so the integral becomes
 .
.
Now we can replace the dummy variable  with any other variable. So we can replace it with the letter
with any other variable. So we can replace it with the letter  to give
to give
 .
.
Now we split the integral into two pieces
 .
.
The proof of the formula for even functions is similar.
Prove that if  is a continuous even function then for any
is a continuous even function then for any  ,
,
 .
.
From the property of linearity of the endpoints we have

Make the substitution  .
.  when
when  and
and  when
when  . Then
. Then

where the last step has used the evenness of  . Since
. Since  is just a dummy variable, we can replace it with
is just a dummy variable, we can replace it with  . Then
. Then

Resources
Licensing
Content obtained and/or adapted from:









![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)











![{\displaystyle [x_{i-1},x_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09cb12a889d47020c8ce7046a2eb60785e00c0b6)









![{\displaystyle x_{i}^{*}\in [x_{i-1},x_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dafeab86f1179399f11208ee27a15c76434aed3d)


















![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)

























































![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)







































