The Definite Integral

Suppose we are given a function and would like to determine the area underneath its graph over an interval. We could guess, but how could we figure out the exact area? Below, using a few clever ideas, we actually define such an area and show that by using what is called the definite integral we can indeed determine the exact area underneath a curve.

Introduction

Figure 1: Approximation of the area under the curve $f(x)$ from $x=x_{0}$ to $x=x_{4}$.

Figure 2: Rectangle approximating the area under the curve from $x_{2}$ to $x_{3}$ with sample point $x_{3}^{*}$ .

The rough idea of defining the area under the graph of $f$ is to approximate this area with a finite number of rectangles. Since we can easily work out the area of the rectangles, we get an estimate of the area under the graph. If we use a larger number of smaller-sized rectangles we expect greater accuracy with respect to the area under the curve and hence a better approximation. Somehow, it seems that we could use our old friend from differentiation, the limit, and "approach" an infinite number of rectangles to get the exact area. Let's look at such an idea more closely.

Suppose we have a function $f$ that is positive on the interval $[a,b]$ and we want to find the area $S$ under $f$ between $a$ and $b$ . Let's pick an integer $n$ and divide the interval into $n$ subintervals of equal width (see Figure 1). As the interval $[a,b]$ has width $b-a$, each subinterval has width $\Delta x={\frac {b-a}{n}}$ . We denote the endpoints of the subintervals by $x_{0},x_{1},\ldots ,x_{n}$ . This gives us

$x_{i}=a+i\Delta x{\text{ for }}i=0,1,\dots ,n$

Figure 3: Riemann sums with an increasing number of subdivisions yielding better approximations.

Now for each $i=1,\ldots ,n$ pick a sample point $x_{i}^{*}$ in the interval $[x_{i-1},x_{i}]$ and consider the rectangle of height $f(x_{i}^{*})$ and width $\Delta x$ (see Figure 2). The area of this rectangle is $f(x_{i}^{*})\Delta x$ . By adding up the area of all the rectangles for $i=1,\ldots ,n$ we get that the area $S$ is approximated by

$A_{n}=f(x_{1}^{*})\Delta x+\dots +f(x_{n}^{*})\Delta x$

A more convenient way to write this is with summation notation.

$A_{n}=\sum _{i=1}^{n}f(x_{i}^{*})\Delta x$

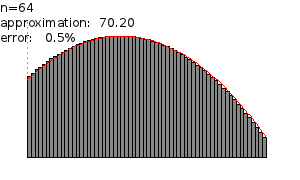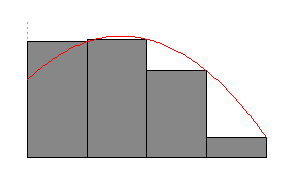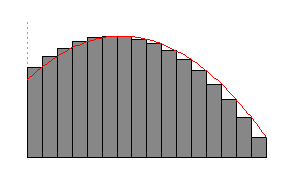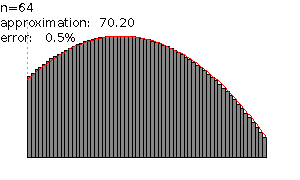
For each number $n$ we get a different approximation. As $n$ gets larger the width of the rectangles gets smaller which yields a better approximation (see Figure 3). In the limit of $A_{n}$ as $n$ tends to infinity we get the area $S$ .

Definition of the Definite Integral

Suppose $f$ is a continuous function on $[a,b]$ and $\Delta x={\frac {b-a}{n}}$ . Then the definite integral of $f$ between $a$ and $b$ is

$\int \limits _{a}^{b}f(x)dx=\lim _{n\to \infty }A_{n}=\lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i}^{*})\Delta x$

where $x_{i}^{*}$ are any sample points in the interval $[x_{i-1},x_{i}]$ and $x_{k}=a+k\cdot \Delta x$ for $k=0,\dots ,n$ .

It is a fact that if $f$ is continuous on $[a,b]$ then this limit always exists and does not depend on the choice of the points $x_{i}^{*}\in [x_{i-1},x_{i}]$ . For instance they may be evenly spaced, or distributed ambiguously throughout the interval. The proof of this is technical and is beyond the scope of this section.

Notation

When considering the expression, $\int \limits _{a}^{b}f(x)dx$ (read "the integral from $a$ to $b$ of the $f$ of $x$ $dx$"), the function $f$ is called the integrand and the interval $[a,b]$ is the interval of integration. Also $a$ is called the lower limit and $b$ the upper limit of integration.

Figure 4: The integral gives the signed area under the graph.

One important feature of this definition is that we also allow functions which take negative values. If $f(x)<0$ for all $x$ then $f(x_{i}^{*})<0$ so $f(x_{i}^{*})\Delta x<0$ . So the definite integral of $f$ will be strictly negative. More generally if $f$ takes on both positive and negative values then $\int \limits _{a}^{b}f(x)dx$ will be the area under the positive part of the graph of $f$ minus the area above the graph of the negative part of the graph (see Figure 4). For this reason we say that $\int \limits _{a}^{b}f(x)dx$ is the signed area under the graph.

Independence of Variable

It is important to notice that the variable $x$ did not play an important role in the definition of the integral. In fact we can replace it with any other letter, so the following are all equal:

$\int \limits _{a}^{b}f(x)dx=\int \limits _{a}^{b}f(t)dt=\int \limits _{a}^{b}f(u)du=\int \limits _{a}^{b}f(w)dw$

Each of these is the signed area under the graph of $f$ between $a$ and $b$ . Such a variable is often referred to as a dummy variable or a bound variable.

Left and Right Handed Riemann Sums

Figure 5: Right-handed Riemann sum

Figure 6: Left-handed Riemann sum

The following methods are sometimes referred to as L-RAM and R-RAM, RAM standing for "Rectangular Approximation Method."

We could have decided to choose all our sample points $x_{i}^{*}$ to be on the right hand side of the interval $[x_{i-1},x_{i}]$ (see Figure 5). Then $x_{i}^{*}=x_{i}$ for all $i$ and the approximation that we called $A_{n}$ for the area becomes

$A_{n}=\sum _{i=1}^{n}f(x_{i})\Delta x$

This is called the right-handed Riemann sum, and the integral is the limit

$\int \limits _{a}^{b}f(x)dx=\lim _{n\to \infty }A_{n}=\lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i})\Delta x$

Alternatively we could have taken each sample point on the left hand side of the interval. In this case $x_{i}^{*}=x_{i-1}$ (see Figure 6) and the approximation becomes

$A_{n}=\sum _{i=1}^{n}f(x_{i-1})\Delta x$

Then the integral of $f$ is

$\int \limits _{a}^{b}f(x)dx=\lim _{n\to \infty }A_{n}=\lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i-1})\Delta x$

The key point is that, as long as $f$ is continuous, these two definitions give the same answer for the integral.

Examples

Example 1
In this example we will calculate the area under the curve given by the graph of $f(x)=x$ for $x$ between 0 and 1. First we fix an integer $n$ and divide the interval $[0,1]$ into $n$ subintervals of equal width. So each subinterval has width

$\Delta x={\frac {1}{n}}$

To calculate the integral we will use the right-handed Riemann sum. (We could have used the left-handed sum instead, and this would give the same answer in the end). For the right-handed sum the sample points are

$x_{i}^{*}=0+i\Delta x={\frac {i}{n}}\quad i=1,\ldots ,n$

Notice that $f(x_{i}^{*})=x_{i}^{*}={\frac {i}{n}}$ . Putting this into the formula for the approximation,

$A_{n}=\sum _{i=1}^{n}f(x_{i}^{*})\Delta x=\sum _{i=1}^{n}f\left({\frac {i}{n}}\right)\Delta x=\sum _{i=1}^{n}{\frac {i}{n}}\cdot {\frac {1}{n}}={\frac {1}{n^{2}}}\sum _{i=1}^{n}i$

Now we use the formula

$\sum _{i=1}^{n}i={\frac {n(n+1)}{2}}$

to get

$A_{n}={\frac {1}{n^{2}}}\cdot {\frac {n(n+1)}{2}}={\frac {n+1}{2n}}$

To calculate the integral of $f$ between $0$ and $1$ we take the limit as $n$ tends to infinity,

$\int \limits _{0}^{1}f(x)dx=\lim _{n\to \infty }{\frac {n+1}{2n}}={\frac {1}{2}}$

Example 2
Next we show how to find the integral of the function $f(x)=x^{2}$ between $x=a$ and $x=b$ . This time the interval $[a,b]$ has width $b-a$ so

$\Delta x={\frac {b-a}{n}}$

Once again we will use the right-handed Riemann sum. So the sample points we choose are

$x_{i}^{*}=a+i\Delta x=a+{\frac {i(b-a)}{n}}$

Thus

$A_{n}$	$=\sum _{i=1}^{n}f(x_{i}^{*})\Delta x$
	$=\sum _{i=1}^{n}f\left(a+{\frac {(b-a)i}{n}}\right)\Delta x$
	$={\frac {b-a}{n}}\sum _{i=1}^{n}\left(a+{\frac {(b-a)i}{n}}\right)^{2}$
	$={\frac {b-a}{n}}\sum _{i=1}^{n}\left(a^{2}+{\frac {2a(b-a)i}{n}}+{\frac {(b-a)^{2}i^{2}}{n^{2}}}\right)$

We have to calculate each piece on the right hand side of this equation. For the first two,

$\sum _{i=1}^{n}a^{2}=a^{2}\sum _{i=1}^{n}1=na^{2}$

$\sum _{i=1}^{n}{\frac {2a(b-a)i}{n}}={\frac {2a(b-a)}{n}}\sum _{i=1}^{n}i={\frac {2a(b-a)}{n}}\cdot {\frac {n(n+1)}{2}}$

For the third sum we have to use a formula

$\sum _{i=1}^{n}i^{2}={\frac {n(n+1)(2n+1)}{6}}$

to get

$\sum _{i=1}^{n}{\frac {(b-a)^{2}i^{2}}{n^{2}}}={\frac {(b-a)^{2}}{n^{2}}}{\frac {n(n+1)(2n+1)}{6}}$

Putting this together

$A_{n}={\frac {b-a}{n}}\left(na^{2}+{\frac {2a(b-a)}{n}}\cdot {\frac {n(n+1)}{2}}+{\frac {(b-a)^{2}}{n^{2}}}{\frac {n(n+1)(2n+1)}{6}}\right)$

Taking the limit as $n$ tend to infinity gives

$\int \limits _{a}^{b}x^{2}dx$	$=(b-a)\left(a^{2}+a(b-a)+{\frac {1}{3}}(b-a)^{2}\right)$
	$=(b-a)\left(a^{2}+ab-a^{2}+{\frac {1}{3}}(b^{2}-2ab+a^{2})\right)$
	$={\frac {1}{3}}(b-a)(b^{2}+ab+a^{2})$
	$={\frac {1}{3}}(b^{3}-a^{3})$

Basic Properties of the Integral

From the definition of the integral we can deduce some basic properties. For all the following rules, suppose that $f$ and $g$ are continuous on $[a,b]$ .

The Constant Rule

Constant Rule: $\int \limits _{a}^{b}c\cdot f(x)dx=c\int \limits _{a}^{b}f(x)dx$

When $f$ is positive, the height of the function $c\cdot f$ at a point $x$ is $c$ times the height of the function $f$ . So the area under $c\cdot f$ between $a$ and $b$ is $c$ times the area under $f$ . We can also give a proof using the definition of the integral, using the constant rule for limits,

$\int \limits _{a}^{b}c\cdot f(x)dx=\lim _{n\to \infty }\sum _{i=1}^{n}c\cdot f(x_{i}^{*})=c\cdot \lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i}^{*})=c\int \limits _{a}^{b}f(x)dx$

Example

We saw in the previous section that

$\int \limits _{0}^{1}xdx={\frac {1}{2}}$

Using the constant rule we can use this to calculate that

$\int \limits _{0}^{1}3xdx=3\int \limits _{0}^{1}xdx=3\cdot {\frac {1}{2}}=1.5$ ,

$\int \limits _{0}^{1}-7xdx=-7\int \limits _{0}^{1}xdx=(-7)\cdot {\frac {1}{2}}=-3.5$ .

Example

We saw in the previous section that

$\int \limits _{a}^{b}x^{2}dx={\frac {b^{3}-a^{3}}{3}}$

We can use this and the constant rule to calculate that

$\int \limits _{1}^{3}2x^{2}dx=2\int \limits _{1}^{3}x^{2}dx=2\cdot {\frac {1}{3}}\cdot (3^{3}-1^{3})={\frac {2}{3}}(27-1)={\frac {52}{3}}$

There is a special case of this rule used for integrating constants:

If $c$ is constant then $\int \limits _{a}^{b}c\ dx=c(b-a)$

When $c>0$ and $a<b$ this integral is the area of a rectangle of height $c$ and width $b-a$ which equals $c(b-a)$ .

Example

$\int \limits _{1}^{3}9dx=9(3-1)=9\cdot 2=18$

$\int \limits _{-2}^{6}11dx=11(6-(-2))=11\cdot 8=88$

$\int \limits _{2}^{17}0dx=0\cdot (17-2)=0$

The addition and subtraction rule

Addition and Subtraction Rules of Integration:

$\int \limits _{a}^{b}{\bigl (}f(x)+g(x){\bigr )}dx=\int \limits _{a}^{b}f(x)dx+\int \limits _{a}^{b}g(x)dx$ $\int \limits _{a}^{b}{\bigl (}f(x)-g(x){\bigr )}dx=\int \limits _{a}^{b}f(x)dx-\int \limits _{a}^{b}g(x)dx$

As with the constant rule, the addition rule follows from the addition rule for limits:

$\int \limits _{a}^{b}{\bigl (}f(x)+g(x){\bigr )}dx$	$=\lim _{n\to \infty }\sum _{i=1}^{n}{\Big (}f(x_{i}^{*})+g(x_{i}^{*}){\Big )}$
	$=\lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i}^{*})+\lim _{n\to \infty }\sum _{i=1}^{n}g(x_{i}^{*})$
	$=\int \limits _{a}^{b}f(x)dx+\int \limits _{a}^{b}g(x)dx$

The subtraction rule can be proved in a similar way.

Example

From above $\int \limits _{1}^{3}9dx=18$ and $\int \limits _{1}^{3}2x^{2}dx={\frac {52}{3}}$ so

$\int \limits _{1}^{3}(2x^{2}+9)dx=\int \limits _{1}^{3}2x^{2}dx+\int \limits _{1}^{3}9dx={\frac {52}{3}}+18={\frac {106}{3}}$

$\int \limits _{1}^{3}(2x^{2}-9)dx=\int \limits _{1}^{3}2x^{2}dx-\int \limits _{1}^{3}9dx={\frac {52}{3}}-18=-{\frac {2}{3}}$

Example

$\int \limits _{0}^{2}(4x^{2}+14)dx=4\int \limits _{0}^{2}x^{2}dx+\int \limits _{0}^{2}14dx=4\cdot {\frac {1}{3}}(2^{3}-0^{3})+2\cdot 14={\frac {32}{3}}+28={\frac {116}{3}}$

The Comparison Rule

Figure 7: Bounding the area under $f(x)$ on $[a,b]$

Comparison Rule:

• Suppose $f(x)\geq 0$ for all $x\in [a,b]$ . Then

$\int \limits _{a}^{b}f(x)dx\geq 0$

• Suppose $f(x)\geq g(x)$ for all $x\in [a,b]$ . Then

$\int \limits _{a}^{b}f(x)dx\geq \int \limits _{a}^{b}g(x)dx$

• Suppose $M\geq f(x)\geq m$ for all $x\in [a,b]$ . Then

$M(b-a)\geq \int \limits _{a}^{b}f(x)dx\geq m(b-a)$

If $f(x)\geq 0$ then each of the rectangles in the Riemann sum to calculate the integral of $f$ will be above the $y$ axis, so the area will be non-negative. If $f(x)\geq g(x)$ then $f(x)-g(x)\geq 0$ and by the first property we get the second property. Finally if $M\geq f(x)\geq m$ then the area under the graph of $f$ will be greater than the area of rectangle with height $m$ and less than the area of the rectangle with height $M$ (see Figure 7). So

$M(b-a)=\int \limits _{a}^{b}M\geq \int \limits _{a}^{b}f(x)dx\geq \int \limits _{a}^{b}m=m(b-a)$

Linearity with respect to endpoints

Additivity with respect to endpoints:

Suppose $a<c<b$ . Then

$\int \limits _{a}^{b}f(x)dx=\int \limits _{a}^{c}f(x)dx+\int \limits _{c}^{b}f(x)dx$

Again suppose that $f$ is positive. Then this property should be interpreted as saying that the area under the graph of $f$ between $a$ and $b$ is the area between $a$ and $c$ plus the area between $c$ and $b$ (see Figure 8).

Figure 8: Illustration of the property of additivity with respect to endpoints

{{Calculus/Def|text= Extension of Additivity with respect to limits of integration
When $a=b$ we have that $\Delta x={\frac {b-a}{n}}=0$ so

$\int \limits _{a}^{a}f(x)dx=0$

Also in defining the integral we assumed that $a<b$ . But the definition makes sense even when $b<a$ , in which case $\Delta x={\frac {b-a}{n}}$ has changed sign. This gives

$\int \limits _{b}^{a}f(x)dx=-\int \limits _{a}^{b}f(x)dx$

With these definitions,

$\int \limits _{a}^{b}f(x)dx=\int \limits _{a}^{c}f(x)dx+\int \limits _{c}^{b}f(x)dx$

whatever the order of $a,b,c$ .

Even and odd functions

Recall that a function $f$ is called odd if it satisfies $f(-x)=-f(x)$ and is called even if $f(-x)=f(x)$ .

Suppose $f$ is a continuous odd function. Then for any $a$,

$\int \limits _{-a}^{a}f(x)dx=0$

If $f$ is a continuous even function then for any $a$,

$\int \limits _{-a}^{a}f(x)dx=2\int \limits _{0}^{a}f(x)dx$

Suppose $f$ is an odd function and consider first just the integral from $-a$ to $0$ . We make the substitution $u=-x$ so $du=-dx$ . Notice that if $x=-a$ then $u=a$ and if $x=0$ then $u=0$ . Hence

$\int \limits _{-a}^{0}f(x)dx=-\int \limits _{a}^{0}f(-u)du=\int \limits _{0}^{a}f(-u)du$ .

Now as $f$ is odd, $f(-u)=-f(u)$ so the integral becomes

$\int \limits _{-a}^{0}f(x)dx=-\int \limits _{0}^{a}f(u)du$ .

Now we can replace the dummy variable $u$ with any other variable. So we can replace it with the letter $x$ to give

$\int \limits _{-a}^{0}f(x)dx=-\int \limits _{0}^{a}f(u)du=-\int \limits _{0}^{a}f(x)dx$ .

Now we split the integral into two pieces

$\int \limits _{-a}^{a}f(x)dx=\int \limits _{-a}^{0}f(x)dx+\int \limits _{0}^{a}f(x)dx=-\int \limits _{0}^{a}f(x)dx+\int \limits _{0}^{a}f(x)dx=0$ .

The proof of the formula for even functions is similar.

Prove that if $f$ is a continuous even function then for any $a$ ,

$\int \limits _{-a}^{a}f(x)dx=2\int \limits _{0}^{a}f(x)dx$.

From the property of linearity of the endpoints we have

$\int \limits _{-a}^{a}f(x)dx=\int \limits _{-a}^{0}f(x)dx+\int \limits _{0}^{a}f(x)dx$

Make the substitution $u=-x;\quad du=-dx$ . $u=a$ when $x=-a$ and $u=0$ when $x=0$ . Then

$\int \limits _{-a}^{0}f(x)dx=\int \limits _{a}^{0}f(-u)(-du)=-\int \limits _{a}^{0}f(-u)du=\int \limits _{0}^{a}f(-u)du=\int \limits _{0}^{a}f(u)du$

where the last step has used the evenness of $f$ . Since $u$ is just a dummy variable, we can replace it with $x$ . Then

$\int \limits _{-a}^{a}f(x)dx=\int \limits _{0}^{a}f(x)dx+\int \limits _{0}^{a}f(x)dx=2\int \limits _{0}^{a}f(x)dx$

Resources

• Distance Definite Integral (Slides 23-38). PowerPoint file created by Professor Cynthia Roberts, UTSA.
• Definite Integral & Antiderivatives. PowerPoint file created by Professor Cynthia Roberts, UTSA.

• The Definite Integral PowerPoint file created by Dr. Sara Shirinkam, UTSA.

• The Definite Integral Notes created by Professor Eduardo Duenez, UTSA.

Licensing

Content obtained and/or adapted from:

• Definite integral, Wikibooks: Calculus under a CC BY-SA license